iEEG Data
Contents
iEEG Data¶
This notebook analyses a large dataset of iEEG data, from the MNI database.
Dataset Details¶
This analysis uses the openly available MNI dataset.
# Setup notebook state
from nbutils import setup_notebook; setup_notebook()
import numpy as np
import matplotlib.pyplot as plt
from fooof import FOOOF, FOOOFGroup
from fooof.plts import plot_spectra
from fooof.analysis import get_band_peak_fg
from neurodsp.utils import create_times
from neurodsp.aperiodic import compute_irasa
from neurodsp.spectral import compute_spectrum, trim_spectrum
from neurodsp.plts import plot_time_series, plot_power_spectra
from neurodsp.plts.utils import make_axes
# Import custom project code
from apm.io import APMDB, get_files, load_pickle
from apm.io.data import load_ieeg_all
from apm.analysis import (compute_all_corrs, unpack_corrs,
compute_corrs_to_feature, compute_diffs_to_feature)
from apm.plts import plot_dots, plot_corr_matrix
from apm.plts.multi import plot_results_all
from apm.plts.utils import figsaver
from apm.plts.settings import LABELS
from apm.utils import format_corr
# Import dataset settings from script
import sys; from pathlib import Path;
sys.path.append(str(Path('..').resolve() / 'scripts'))
from scripts.analyze_ieeg import (DATA_FOLDER, NON_CORTICAL, FS, MAX_TIME,
FIT_RANGE_SHORT, FIT_RANGE_LONG)
from scripts.settings import SPECPARAM_SETTINGS, SPECPARAM_SETTINGS_KNEE
Set Up Paths¶
# Define load path
db = APMDB()
LOADPATH = db.data_path / 'ieeg'
# Check the set of results files available for this dataset
get_files(LOADPATH)
['ieeg_all_corrs.p',
'ieeg_results.p',
'ieeg_specparam.json',
'ieeg_specparam_long.json',
'ieeg_specparam_short.json']
Settings¶
# Define band range for peaks
peak_range = [2, 35]
# Add plot kwargs
dot_kwargs = {
's' : 16,
'alpha' : 0.4,
}
# Settings for saving figures
SAVE_FIG = True
FIGPATH = db.figs_path / '53_ieeg_data'
# Create helper function to manage figsaver settings
fsaver = figsaver(SAVE_FIG, FIGPATH)
Load Data¶
# Get the list of available files
files = get_files(DATA_FOLDER)
# Check the number of files
n_files = len(files)
print('Number of files: {}'.format(n_files))
Number of files: 38
# Load all data files
all_data, all_chs = load_ieeg_all(files, DATA_FOLDER, MAX_TIME, NON_CORTICAL, return_channels=True)
# Create times definition
times = create_times(MAX_TIME, FS)
# Check data size
n_chs, n_times = all_data.shape
print('Number of channels: {}'.format(n_chs))
Number of channels: 1479
Data Checks¶
# Set example channel index
chi = 550
# Plot an example time series
plot_time_series(times, all_data[chi, :], lw=1., figsize=(12, 1))
plt.gca().axis('off');

# Plot a zoomed in segment of a time series
plot_time_series(times, all_data[chi, :], xlim=[5, 12], lw=1., figsize=(12, 1))
plt.gca().axis('off');
if SAVE_FIG: plt.savefig(FIGPATH / ('ieeg_timeseries.pdf'))

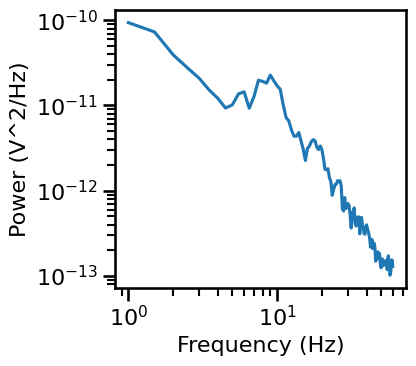
# Compute a power spectrum of an example
freqs, powers = compute_spectrum(all_data[chi, :], FS, nperseg=2*FS, noverlap=FS)
# Trim spectrum to fit range
freqs, powers = trim_spectrum(freqs, powers, FIT_RANGE_LONG)
# Plot the power spectrum
plot_power_spectra(freqs, powers, figsize=(4.5, 4), **fsaver('ieeg_psd'))
Check Spectral Fits - Short Fit Range¶
# Load specparam measures
fg_short = FOOOFGroup()
fg_short.load('ieeg_specparam_short', LOADPATH)
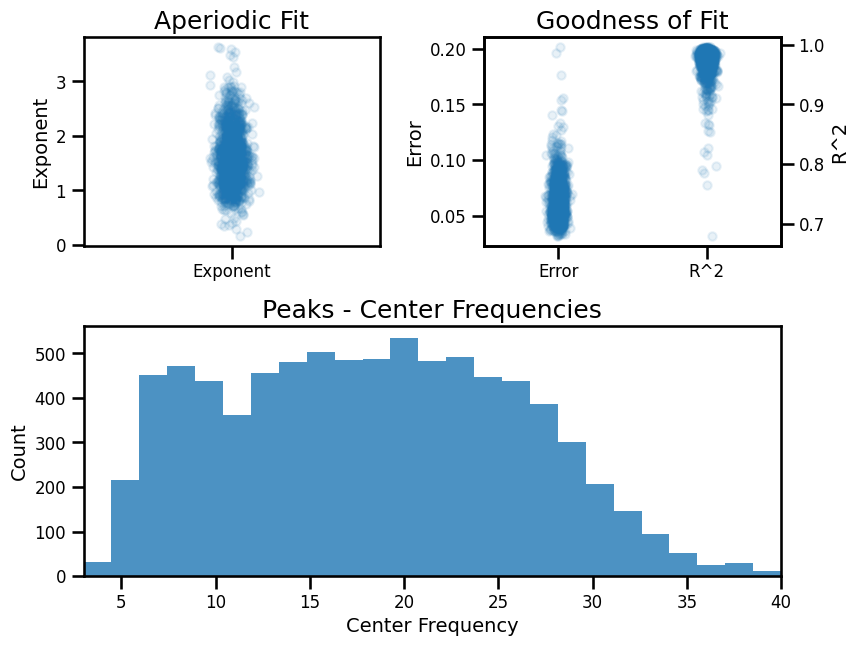
# Check overall group results
fg_short.print_results()
fg_short.plot()
==================================================================================================
FOOOF - GROUP RESULTS
Number of power spectra in the Group: 1479
The model was run on the frequency range 3 - 40 Hz
Frequency Resolution is 0.50 Hz
Power spectra were fit without a knee.
Aperiodic Fit Values:
Exponents - Min: 0.162, Max: 3.640, Mean: 1.599
In total 8033 peaks were extracted from the group
Goodness of fit metrics:
R2s - Min: 0.679, Max: 0.997, Mean: 0.973
Errors - Min: 0.032, Max: 0.202, Mean: 0.064
==================================================================================================
Example Spectral Model - Short Fit Range¶
# Set example channel index
chi = 550
# Compute a power spectrum of an example signal, and trim to fit range
freqs, powers = compute_spectrum(all_data[chi, :], FS, nperseg=2*FS, noverlap=FS)
freqs, powers = trim_spectrum(freqs, powers, FIT_RANGE_SHORT)
# Fit a spectral model to example data
fm = FOOOF(**SPECPARAM_SETTINGS)
fm.fit(freqs, powers, FIT_RANGE_SHORT)
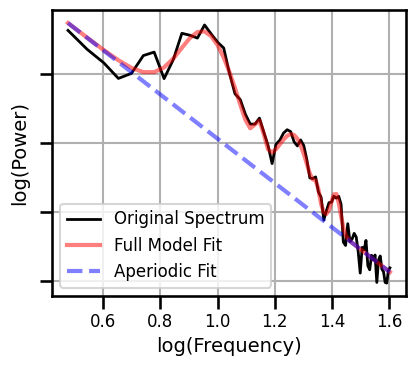
# Plot the specparam spectral model
fm.plot(plt_log=True, figsize=(4.5, 4), yticklabels=[],
**fsaver('ieeg_spectral_model_short'))
IRASA¶
# Compute the IRASA decomposition
freqs_ir, psd_ap, psd_pe = compute_irasa(all_data[chi, :], FS, FIT_RANGE_SHORT)
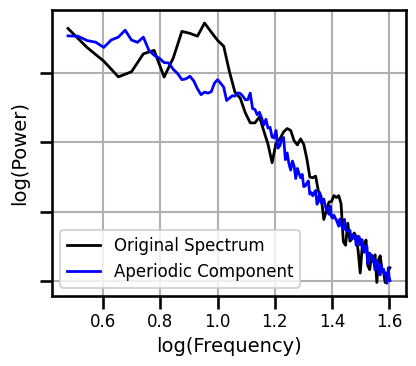
# Plot the IRASA data & aperiodic component
plot_spectra([freqs, freqs_ir], [powers, psd_ap], log_freqs=True, figsize=(4.5, 4),
log_powers=True, colors=['black', 'blue'], yticklabels=[],
labels=['Original Spectrum', 'Aperiodic Component'],
**fsaver('ieeg_irasa_model_short'))
Check Spectral Fits - Long Fit Range¶
# Load specparam measures
fg_long = FOOOFGroup()
fg_long.load('ieeg_specparam_long', LOADPATH)
# Check overall group results
fg_long.print_results()
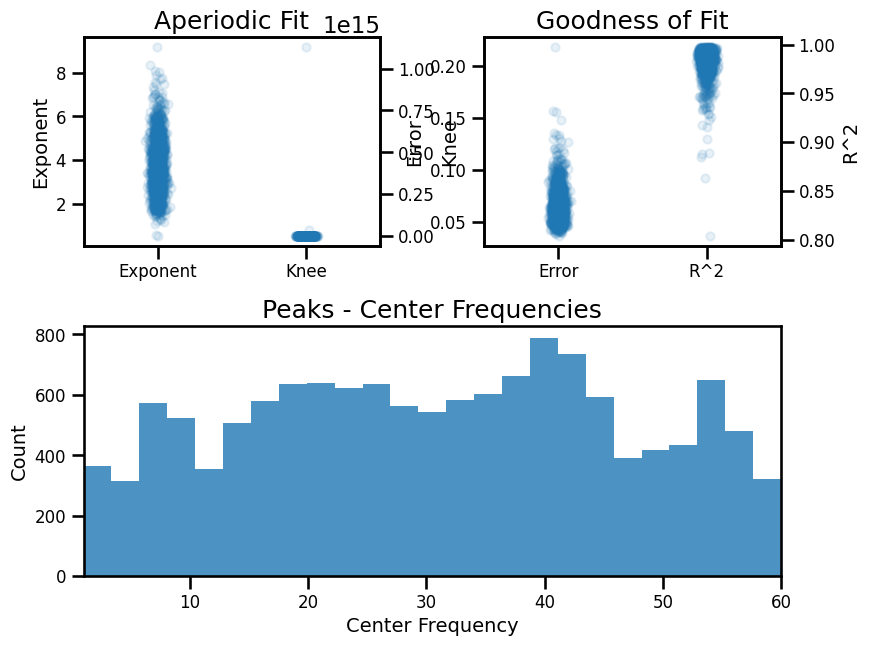
fg_long.plot()
==================================================================================================
FOOOF - GROUP RESULTS
Number of power spectra in the Group: 1479
The model was run on the frequency range 1 - 60 Hz
Frequency Resolution is 0.50 Hz
Power spectra were fit with a knee.
Aperiodic Fit Values:
Knees - Min: -0.93, Max: 1131368032417823.25, Mean: 791471350711.19
Exponents - Min: 0.511, Max: 9.205, Mean: 3.741
In total 13524 peaks were extracted from the group
Goodness of fit metrics:
R2s - Min: 0.803, Max: 0.998, Mean: 0.984
Errors - Min: 0.036, Max: 0.219, Mean: 0.066
==================================================================================================
Example Spectral Model - Long Fit Range¶
# Set example channel index
chi = 813
# Compute a power spectrum of an example signal, and trim to fit rante
freqs, powers = compute_spectrum(all_data[chi, :], FS, nperseg=2*FS, noverlap=FS)
freqs, powers = trim_spectrum(freqs, powers, FIT_RANGE_LONG)
# Fit a spectral model to example data
fm = FOOOF(**SPECPARAM_SETTINGS_KNEE)
fm.fit(freqs, powers, FIT_RANGE_LONG)
/Users/tom/opt/anaconda3/envs/apm/lib/python3.9/site-packages/scipy/optimize/_lsq/trf.py:234: RuntimeWarning: divide by zero encountered in divide
Delta = norm(x0 * scale_inv / v**0.5)
/Users/tom/opt/anaconda3/envs/apm/lib/python3.9/site-packages/scipy/optimize/_lsq/trf.py:363: RuntimeWarning: invalid value encountered in scalar divide
alpha *= Delta / Delta_new
/Users/tom/opt/anaconda3/envs/apm/lib/python3.9/site-packages/scipy/optimize/_lsq/common.py:49: RuntimeWarning: invalid value encountered in scalar divide
t2 = c / q
/Users/tom/opt/anaconda3/envs/apm/lib/python3.9/site-packages/scipy/optimize/_lsq/trf.py:363: RuntimeWarning: invalid value encountered in scalar multiply
alpha *= Delta / Delta_new
/Users/tom/opt/anaconda3/envs/apm/lib/python3.9/site-packages/scipy/optimize/_lsq/common.py:398: RuntimeWarning: invalid value encountered in cast
return min_step, np.equal(steps, min_step) * np.sign(s).astype(int)
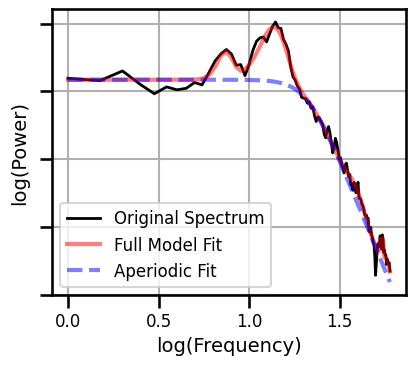
# Plot the specparam spectral model
fm.plot(plt_log=True, figsize=(4.5, 4), yticklabels=[],
**fsaver('ieeg_spectral_model_long'))
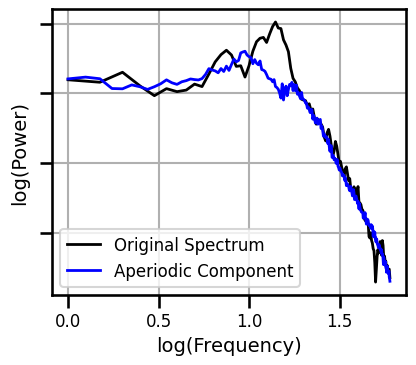
IRASA¶
# Compute the IRASA decomposition
freqs_ir, psd_ap, psd_pe = compute_irasa(all_data[chi, :], FS, FIT_RANGE_LONG)
# Plot the IRASA data & aperiodic component
plot_spectra([freqs, freqs_ir], [powers, psd_ap], log_freqs=True, figsize=(4.5, 4),
log_powers=True, colors=['black', 'blue'], yticklabels=[],
labels=['Original Spectrum', 'Aperiodic Component'],
**fsaver('ieeg_irasa_model_long'))
Load Results¶
# Load precomputed aperiodic measure results
results = load_pickle('ieeg_results', LOADPATH)
# Check size of computed results [n_chs]
results['dfa'].shape
(1479,)
Check Measures & Labels¶
# Check list of computed measures
print(list(results.keys()))
['autocorr_decay_time', 'dfa', 'higuchi_fd', 'hjorth_complexity', 'lempelziv', 'sample_entropy', 'perm_entropy', 'specparam_short', 'specparam_long', 'specparam_knee', 'specparam_knee_freq', 'irasa_short', 'irasa_long', 'irasa_knee', 'irasa_knee_freq']
# Collect list of exponent & timeseries measure labels
exp_measures = ['specparam_short', 'specparam_long', 'irasa_short', 'irasa_long']
knee_measures = ['specparam_knee', 'specparam_knee_freq', 'irasa_knee', 'irasa_knee_freq']
ts_measures = list(results.keys())
[ts_measures.remove(meas) for meas in exp_measures + knee_measures];
# Collect labels for time series measures
ts_labels = [LABELS[meas] for meas in ts_measures]
Compute Correlations¶
# Load precomputed aperiodic measure results
all_corrs = load_pickle('ieeg_all_corrs', LOADPATH)
# # Compute correlations across all pairs of methods
# all_corrs = compute_all_corrs(results)
Compare exponent measures - short¶
# Check exponent data ranges
print('SP: {:1.2f}-{:1.2f}'.format(np.min(results['specparam_short']),
np.max(results['specparam_short'])))
print('IR: {:1.2f}-{:1.2f}'.format(np.min(results['irasa_short']),
np.max(results['irasa_short'])))
SP: 0.16-3.64
IR: 0.13-4.03
# Compare aperiodic exponent from specparam & IRASA
plot_dots(results['specparam_short'], results['irasa_short'], alpha=0.25, tposition='tl',
xlim=[0, 4.5], ylim=[0, 4.5], expected=[0, 4.5], s=10, figsize=(4.5, 4),
xlabel='Aperiodic Exponent (SP)', ylabel='Aperiodic Exponent (IR)',
**fsaver('ieeg_exp_exp_short'))
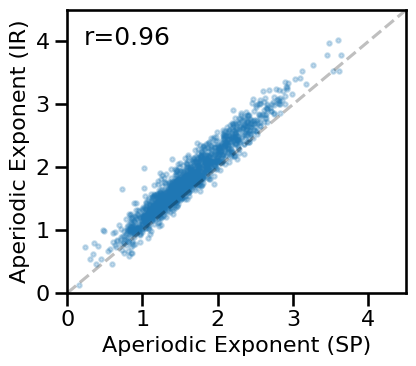
# Check correlation between exponent estimates
print(' SP-EXP & IR-EXP: ', format_corr(*all_corrs['specparam_short']['irasa_short']))
SP-EXP & IR-EXP: r=+0.956 CI[+0.949, +0.962], p=0.000
# Compute average difference between exponent estimates
exp_diffs_short = np.abs(results['specparam_short'] - results['irasa_short'])
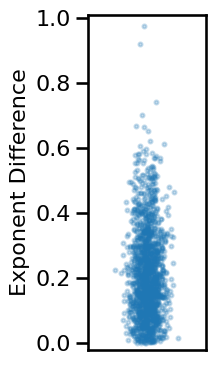
# Plot the distribution of differences between exponent measures
plot_dots(np.random.randn(len(exp_diffs_short)) * 0.15, exp_diffs_short,
add_corr=False, figsize=(2.5, 4), xticks=[], xlim=[-1, 1],
ylim=[-0.02, 1.01], ylabel='Exponent Difference', alpha=0.25, s=8,
**fsaver('ieeg_exp_diffs'))
# Check median and range of exponent differences
print('Median exp diff: \t{:1.2f}'.format(np.median(exp_diffs_short)))
print('Min/Max: \t\t{:1.2f}, {:1.2f}'.format(np.min(exp_diffs_short),
np.max(exp_diffs_short)))
Median exp diff: 0.19
Min/Max: 0.00, 0.97
Compare exponent measures - long¶
# Check exponent data ranges
print('SP: {:1.2f}-{:1.2f}'.format(np.min(results['specparam_long']),
np.max(results['specparam_long'])))
print('IR: {:1.2f}-{:1.2f}'.format(np.min(results['irasa_long']),
np.max(results['irasa_long'])))
SP: 0.51-9.21
IR: 0.49-9.98
# Compare aperiodic exponent from specparam & IRASA
plot_dots(results['specparam_long'], results['irasa_long'], alpha=0.25, tposition='tl',
xlim=[0, 8.6], ylim=[0, 8.6], expected=[0, 8.6], s=10, figsize=(4.5, 4),
xlabel='Aperiodic Exponent (SP)', ylabel='Aperiodic Exponent (IR)',
**fsaver('ieeg_exp_exp_long'))
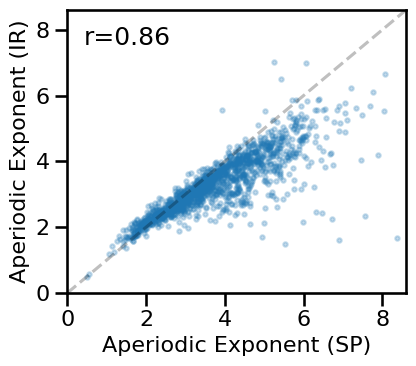
# Check correlation between exponent estimates
print(' SP-EXP & IR-EXP: ', format_corr(*all_corrs['specparam_long']['irasa_long']))
SP-EXP & IR-EXP: r=+0.862 CI[+0.836, +0.886], p=0.000
# Compute average difference between exponent estimates
exp_diffs_long = np.abs(results['specparam_long'] - results['irasa_long'])
# Plot the distribution of differences between exponent measures
plot_dots(np.random.randn(len(exp_diffs_long)) * 0.15, exp_diffs_long, add_corr=False,
xticks=[], xlim=[-1, 1], ylim=[-0.1, 5.5], ylabel='Exponent Difference',
alpha=0.25, s=8, figsize=(2.5, 4), **fsaver('ieeg_exp_diffs'))
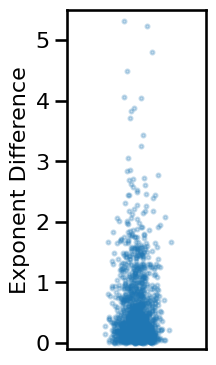
# Check median and range of exponent differences
print('Median exp diff: \t{:1.2f}'.format(np.median(exp_diffs_long)))
print('Min/Max: \t\t{:1.2f}, {:1.2f}'.format(np.min(exp_diffs_long),
np.max(exp_diffs_long)))
Median exp diff: 0.30
Min/Max: 0.00, 6.86
Compare knee measures¶
# Check knee data ranges
print('SP: {:1.2f}-{:1.2f}'.format(np.min(results['specparam_knee_freq']),
np.max(results['specparam_knee_freq'])))
print('IR: {:1.2f}-{:1.2f}'.format(np.min(results['irasa_knee_freq']),
np.max(results['irasa_knee_freq'])))
SP: 0.00-43.18
IR: 0.00-34.10
# Compare aperiodic exponent from specparam & IRASA
plot_dots(results['specparam_knee_freq'], results['irasa_knee_freq'], alpha=0.25, tposition='tl',
xlim=[-0.75, 45], ylim=[-0.75, 45], expected=[-0, 45], s=10, figsize=(4.5, 4),
xlabel='Knee Frequency (SP)', ylabel='Knee Frequency (IR)', **fsaver('ieeg_knee_knee'))
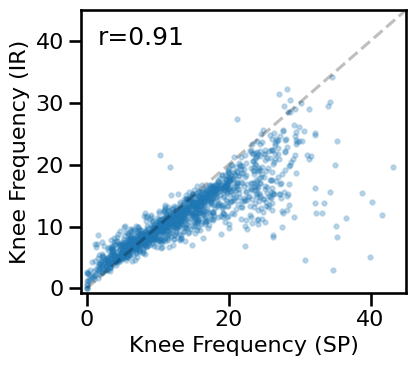
# Check correlation between knee estimates
print(' SP-KNEE & IR-KNEE: ', format_corr(*all_corrs['specparam_knee_freq']['irasa_knee_freq']))
SP-KNEE & IR-KNEE: r=+0.908 CI[+0.890, +0.924], p=0.000
# Compute average difference between knee estimates
knee_diffs = np.abs(results['specparam_knee_freq'] - results['irasa_knee_freq'])
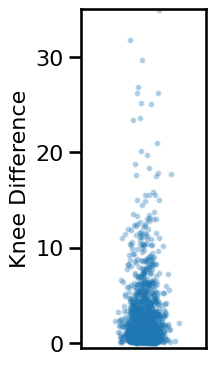
# Plot the distribution of differences between knee measures
plot_dots(np.random.randn(len(knee_diffs)) * 0.15, knee_diffs, add_corr=False,
xticks=[], xlim=[-1, 1], ylim=[-0.5, 35], figsize=(2.5, 4),
ylabel='Knee Difference', alpha=0.25, s=8, **fsaver('ieeg_knee_diffs'))
# Check median and range of knee differences
print('Median exp diff: \t{:1.2f}'.format(np.median(knee_diffs)))
print('Min/Max: \t\t{:1.2f}, {:1.2f}'.format(np.min(knee_diffs), np.max(knee_diffs)))
Median exp diff: 1.62
Min/Max: 0.00, 34.93
Compare Parameters Within Method¶
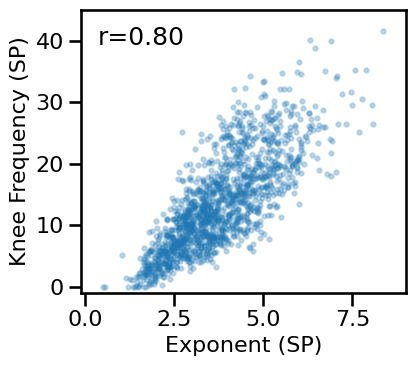
# Compare aperiodic parameters from within each method - specparam
plot_dots(results['specparam_long'], results['specparam_knee_freq'], alpha=0.25, tposition='tl',
xlim=[-0.1, 9], ylim=[-1, 45], s=10, figsize=(4.5, 4), xlabel='Exponent (SP)',
ylabel='Knee Frequency (SP)', **fsaver('ieeg_specparam_params'))
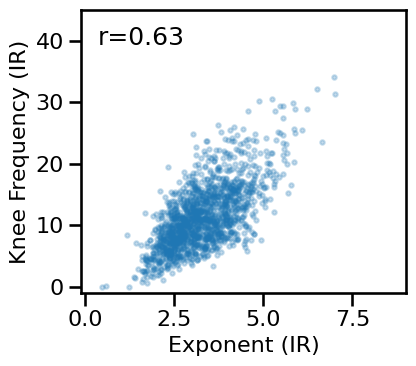
# Compare aperiodic parameters from within each method - irasa
plot_dots(results['irasa_long'], results['irasa_knee_freq'], alpha=0.25, tposition='tl',
xlim=[-0.1, 9], ylim=[-1, 45], s=10, figsize=(4.5, 4), xlabel='Exponent (IR)',
ylabel='Knee Frequency (IR)', **fsaver('ieeg_irasa_params'))
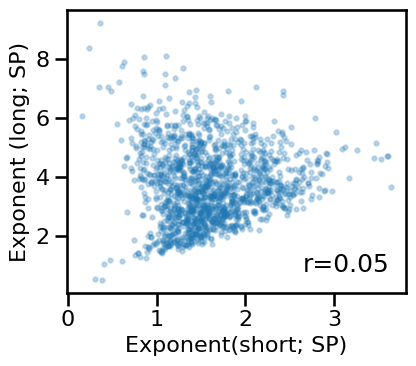
Compare Different Exponents¶
# Compare exponent estimates from within method / across ranges - specparam
plot_dots(results['specparam_short'], results['specparam_long'], alpha=0.25,
tposition='br', s=10, figsize=(4.5, 4), xlabel='Exponent(short; SP)',
ylabel='Exponent (long; SP)', **fsaver('ieeg_specparam_exps'))
# Compare exponent estimates from within method / across ranges - irasa
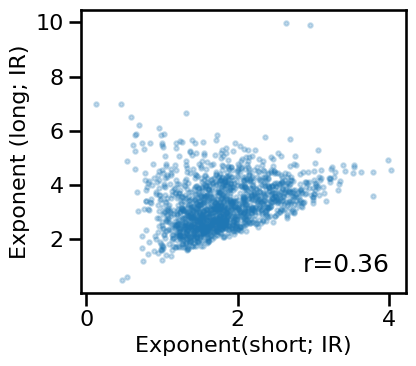
plot_dots(results['irasa_short'], results['irasa_long'], alpha=0.25,
tposition='br', s=10, figsize=(4.5, 4), xlabel='Exponent(short; IR)',
ylabel='Exponent (long; IR)', **fsaver('ieeg_irasa_exps'))
Compare exponent to other measures - long¶
# Plot comparisons between exponent and time series measures
axes = make_axes(1, len(ts_measures), figsize=(26, 4), wspace=0.4)
for ind, meas in enumerate(ts_measures):
plot_dots(results['specparam_short'], results[meas], **dot_kwargs,
xlabel='Aperiodic Exponent', ylabel=LABELS[meas], ax=axes[ind])

# Check the correlations between time series and exponent measures
for meas in ts_measures:
print(meas)
print(' SP-EXP: ', format_corr(*all_corrs['specparam_short'][meas]))
print(' IR-EXP: ', format_corr(*all_corrs['irasa_short'][meas]))
autocorr_decay_time
SP-EXP: r=+0.486 CI[+0.441, +0.527], p=0.000
IR-EXP: r=+0.430 CI[+0.384, +0.474], p=0.000
dfa
SP-EXP: r=-0.082 CI[-0.132, -0.033], p=0.002
IR-EXP: r=-0.179 CI[-0.227, -0.130], p=0.000
higuchi_fd
SP-EXP: r=-0.885 CI[-0.898, -0.870], p=0.000
IR-EXP: r=-0.963 CI[-0.968, -0.957], p=0.000
hjorth_complexity
SP-EXP: r=+0.459 CI[+0.416, +0.500], p=0.000
IR-EXP: r=+0.394 CI[+0.347, +0.438], p=0.000
lempelziv
SP-EXP: r=-0.848 CI[-0.865, -0.829], p=0.000
IR-EXP: r=-0.858 CI[-0.874, -0.840], p=0.000
sample_entropy
SP-EXP: r=-0.796 CI[-0.819, -0.770], p=0.000
IR-EXP: r=-0.837 CI[-0.858, -0.815], p=0.000
perm_entropy
SP-EXP: r=-0.595 CI[-0.628, -0.558], p=0.000
IR-EXP: r=-0.668 CI[-0.699, -0.635], p=0.000
Compare exponent to other measures - long¶
# Plot comparisons between exponent and time series measures
axes = make_axes(1, len(ts_measures), figsize=(26, 4), wspace=0.4)
for ind, meas in enumerate(ts_measures):
plot_dots(results['specparam_long'], results[meas], **dot_kwargs,
xlabel='Aperiodic Exponent', ylabel=LABELS[meas], ax=axes[ind])
if SAVE_FIG: plt.savefig(FIGPATH / ('ieeg_exp_ts_scatters.pdf'))

# Check the correlations between time series and exponent measures
for meas in ts_measures:
print(meas)
print(' SP-EXP: ', format_corr(*all_corrs['specparam_long'][meas]))
print(' IR-EXP: ', format_corr(*all_corrs['irasa_long'][meas]))
autocorr_decay_time
SP-EXP: r=-0.508 CI[-0.549, -0.467], p=0.000
IR-EXP: r=-0.383 CI[-0.429, -0.334], p=0.000
dfa
SP-EXP: r=-0.510 CI[-0.550, -0.468], p=0.000
IR-EXP: r=-0.604 CI[-0.636, -0.570], p=0.000
higuchi_fd
SP-EXP: r=-0.132 CI[-0.185, -0.078], p=0.000
IR-EXP: r=-0.426 CI[-0.472, -0.377], p=0.000
hjorth_complexity
SP-EXP: r=-0.691 CI[-0.721, -0.658], p=0.000
IR-EXP: r=-0.568 CI[-0.607, -0.526], p=0.000
lempelziv
SP-EXP: r=+0.071 CI[+0.021, +0.123], p=0.006
IR-EXP: r=-0.163 CI[-0.212, -0.111], p=0.000
sample_entropy
SP-EXP: r=-0.250 CI[-0.296, -0.202], p=0.000
IR-EXP: r=-0.482 CI[-0.520, -0.442], p=0.000
perm_entropy
SP-EXP: r=-0.684 CI[-0.713, -0.653], p=0.000
IR-EXP: r=-0.871 CI[-0.882, -0.857], p=0.000
Compare knee to other measures¶
# Plot comparisons between knee and time series measures
axes = make_axes(1, len(ts_measures), figsize=(26, 4), wspace=0.4)
for ind, meas in enumerate(ts_measures):
plot_dots(results['specparam_knee_freq'], results[meas], **dot_kwargs,
xlabel='Knee Frequency', ylabel=LABELS[meas], ax=axes[ind])
if SAVE_FIG: plt.savefig(FIGPATH / ('ieeg_knee_ts_scatters.pdf'))

# Check the correlations between time series and knee measures
for meas in ts_measures:
print(meas)
print(' KNEE: \t', format_corr(*all_corrs['specparam_knee'][meas]))
print(' KNEE-FREQ: \t', format_corr(*all_corrs['specparam_knee_freq'][meas]))
autocorr_decay_time
KNEE: r=-0.641 CI[-0.677, -0.603], p=0.000
KNEE-FREQ: r=-0.730 CI[-0.762, -0.695], p=0.000
dfa
KNEE: r=-0.496 CI[-0.539, -0.453], p=0.000
KNEE-FREQ: r=-0.409 CI[-0.454, -0.362], p=0.000
higuchi_fd
KNEE: r=+0.081 CI[+0.025, +0.136], p=0.002
KNEE-FREQ: r=+0.344 CI[+0.290, +0.397], p=0.000
hjorth_complexity
KNEE: r=-0.786 CI[-0.811, -0.759], p=0.000
KNEE-FREQ: r=-0.793 CI[-0.816, -0.768], p=0.000
lempelziv
KNEE: r=+0.290 CI[+0.240, +0.337], p=0.000
KNEE-FREQ: r=+0.531 CI[+0.487, +0.573], p=0.000
sample_entropy
KNEE: r=-0.036 CI[-0.087, +0.015], p=0.170
KNEE-FREQ: r=+0.237 CI[+0.185, +0.288], p=0.000
perm_entropy
KNEE: r=-0.505 CI[-0.543, -0.464], p=0.000
KNEE-FREQ: r=-0.216 CI[-0.265, -0.164], p=0.000
Compare Time Series Measures to Each Other¶
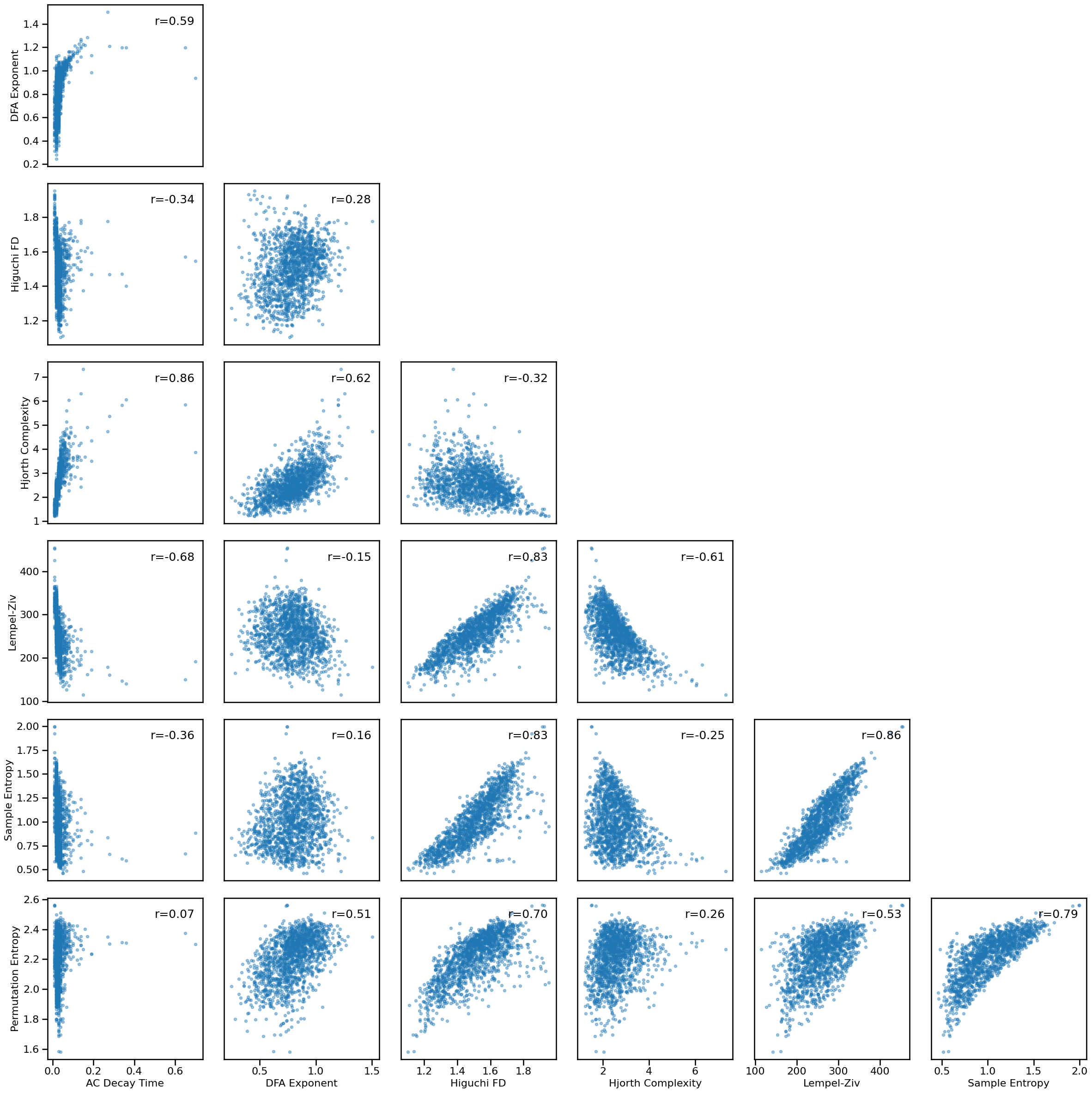
# Plot multi-panel plot comparing all time series measures to each other
plot_results_all(results, ts_measures, **dot_kwargs)
Correlations¶
# Subselect time domain measures
all_corrs_ts = {ke : va for ke, va in all_corrs.items() if ke not in exp_measures + knee_measures}
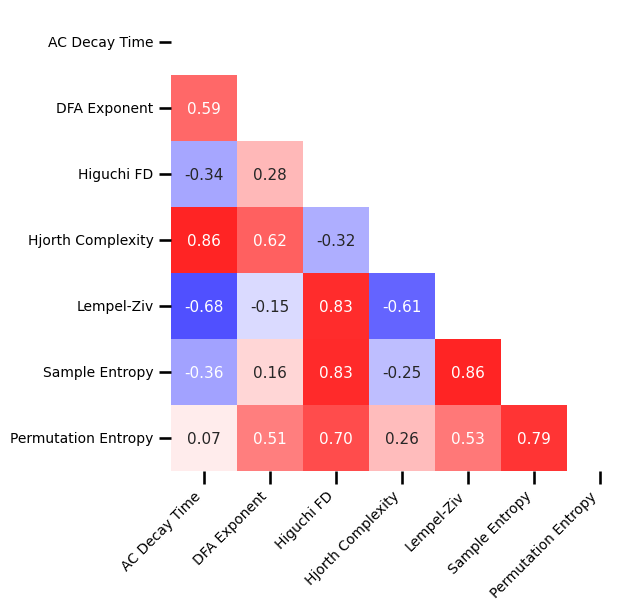
# Plot the correlations matrix across all time series measures
plot_corr_matrix(unpack_corrs(all_corrs_ts), cbar=False, figsize=(6, 6),
xticklabels=ts_labels, yticklabels=ts_labels, **fsaver('ieeg_ts_corr_mat'))
Exponent Correlations¶
# Extract the correlations between specparam and time domain measures
exp_corrs_short = np.atleast_2d([all_corrs['specparam_short'][label][0] for label in ts_measures]).T
# Plot correlations between exponent and time domain measures
plot_corr_matrix(exp_corrs_short, cbar=False, **fsaver('ieeg_exp_corrs_short'))

# Extract the correlations between specparam and time domain measures
exp_corrs_long = np.atleast_2d([all_corrs['specparam_long'][label][0] for label in ts_measures]).T
# Plot correlations between exponent and time domain measures
plot_corr_matrix(exp_corrs_long, cbar=False, **fsaver('ieeg_exp_corrs_long'))

Knee Correlations¶
# Extract the correlations between knee and time domain measures
knee_corrs = np.atleast_2d([all_corrs['specparam_knee_freq'][label][0] for label in ts_measures]).T
# Plot correlations between knee and time domain measures
plot_corr_matrix(knee_corrs, cbar=False, **fsaver('ieeg_knee_corrs'))

Compare to Peaks¶
Short Fit Range¶
# Get peak powers
peak_powers_short = get_band_peak_fg(fg_short, peak_range)[:, 1]
# Check number of nan values
print('# of nan: {}'.format(sum(np.isnan(peak_powers_short))))
# of nan: 0
# Replace nan values with zeros
peak_powers = np.nan_to_num(peak_powers_short)
# Compute correlations between aperiodic measures and peak powers
peak_corrs_short = compute_corrs_to_feature(results, peak_powers_short)
# # Compute differences between correlations between aperiodic measures and peak powers
# peak_corr_diffs = compute_diffs_to_feature(results, peak_powers)
# Check the correlations between peak powers and aperiodic measures
print('Correlations with peak powers:')
for label in peak_corrs_short.keys():
print(' {:20s}: '.format(label), format_corr(*peak_corrs_short[label]))
Correlations with peak powers:
autocorr_decay_time : r=-0.345 CI[-0.390, -0.299], p=0.000
dfa : r=-0.598 CI[-0.632, -0.563], p=0.000
higuchi_fd : r=-0.442 CI[-0.487, -0.397], p=0.000
hjorth_complexity : r=-0.478 CI[-0.517, -0.436], p=0.000
lempelziv : r=-0.190 CI[-0.237, -0.140], p=0.000
sample_entropy : r=-0.441 CI[-0.482, -0.399], p=0.000
perm_entropy : r=-0.729 CI[-0.754, -0.703], p=0.000
specparam_short : r=+0.222 CI[+0.174, +0.270], p=0.000
specparam_long : r=+0.648 CI[+0.615, +0.678], p=0.000
specparam_knee : r=+0.567 CI[+0.529, +0.603], p=0.000
specparam_knee_freq : r=+0.394 CI[+0.348, +0.439], p=0.000
irasa_short : r=+0.330 CI[+0.283, +0.374], p=0.000
irasa_long : r=+0.769 CI[+0.745, +0.792], p=0.000
irasa_knee : r=+0.709 CI[+0.681, +0.737], p=0.000
irasa_knee_freq : r=+0.480 CI[+0.437, +0.520], p=0.000
# Organize correlations between peak powers and time domain measures
peak_corrs_ts_short = np.atleast_2d([peak_corrs_short[label][0] for label in ts_measures]).T
# Plot correlations between peak powers and time domain measures
plot_corr_matrix(peak_corrs_ts_short, cbar=False, **fsaver('ieeg_peak_corrs_short'))

Long Fit Range¶
# Get peak powers
peak_powers_long = get_band_peak_fg(fg_long, peak_range)[:, 1]
# Check number of nan values
print('# of nan: {}'.format(sum(np.isnan(peak_powers_long))))
# of nan: 2
# Replace nan values with zeros
peak_powers_long = np.nan_to_num(peak_powers_long)
# Compute correlations between aperiodic measures and peak powers
peak_corrs_long = compute_corrs_to_feature(results, peak_powers_long)
# Check the correlations between peak powers and aperiodic measures
print('Correlations with peak powers:')
for label in peak_corrs_long.keys():
print(' {:20s}: '.format(label), format_corr(*peak_corrs_long[label]))
Correlations with peak powers:
autocorr_decay_time : r=-0.251 CI[-0.299, -0.205], p=0.000
dfa : r=-0.482 CI[-0.524, -0.439], p=0.000
higuchi_fd : r=-0.194 CI[-0.247, -0.142], p=0.000
hjorth_complexity : r=-0.357 CI[-0.400, -0.311], p=0.000
lempelziv : r=-0.053 CI[-0.103, -0.004], p=0.042
sample_entropy : r=-0.211 CI[-0.258, -0.164], p=0.000
perm_entropy : r=-0.407 CI[-0.450, -0.363], p=0.000
specparam_short : r=+0.019 CI[-0.031, +0.071], p=0.456
specparam_long : r=+0.349 CI[+0.304, +0.392], p=0.000
specparam_knee : r=+0.321 CI[+0.276, +0.365], p=0.000
specparam_knee_freq : r=+0.256 CI[+0.210, +0.300], p=0.000
irasa_short : r=+0.104 CI[+0.053, +0.154], p=0.000
irasa_long : r=+0.386 CI[+0.343, +0.429], p=0.000
irasa_knee : r=+0.364 CI[+0.320, +0.407], p=0.000
irasa_knee_freq : r=+0.268 CI[+0.220, +0.314], p=0.000
# Organize correlations between peak powers and time domain measures
peak_corrs_ts_long = np.atleast_2d([peak_corrs_long[label][0] for label in ts_measures]).T
# Plot correlations between peak powers and time domain measures
plot_corr_matrix(peak_corrs_ts_long, cbar=False, **fsaver('ieeg_peak_corrs_long'))

Conclusions¶
The iEEG data broadly replicates analyses on the EEG datasets.