Multiscale Entropy¶

This notebooks runs multiscale entropy metrics on time series signals.

This notebook includes:

multiscale approximate entropy
multiscale sample entropy
multiscale permutation entropy
multiscale weighted permutation entropy

# Setup notebook state
from nbutils import setup_notebook; setup_notebook()

from neurodsp.sim import sim_powerlaw, sim_synaptic_current, sim_combined
from neurodsp.utils import set_random_seed

# Import custom project code
from apm.io import APMDB
from apm.run import run_sims_load
from apm.run import run_sims_parallel as run_sims
from apm.methods import (multi_sample_entropy, multi_app_entropy,
                         multi_perm_entropy, multi_wperm_entropy)
from apm.methods.settings import (MAP_ENT_PARAMS, MSA_ENT_PARAMS,
                                  MPE_ENT_PARAMS, MWPE_ENT_PARAMS)
from apm.plts.sims import plot_ap_sims, plot_pe_sims, plot_sims_two
from apm.plts.settings import COLORS
from apm.plts.utils import figsaver
from apm.sim.examples import get_examples, check_examples
from apm.sim.settings import N_SIMS
from apm.sim.defs import SIM_ITERS

Settings¶

# Get current sampling rate
fs = SIM_ITERS.fs

# Settings for saving figures
SAVE_FIG = True
FIGPATH = APMDB().figs_path / '25b_multiscale_entropy'

# Create helper function to manage figsaver settings
fsaver = figsaver(SAVE_FIG, FIGPATH)

# Set the random seed
set_random_seed(111)

# Define collection of example signals
examples = get_examples()

Multiscale Entropy¶

# Check settings for entropy measures
print('Multiscale Approximate Entropy:\t\t', MAP_ENT_PARAMS)
print('Multiscale Sample Entropy:\t\t', MSA_ENT_PARAMS)
print('Multiscale Permutation Entropy:\t\t', MPE_ENT_PARAMS)
print('Multiscale WPermutation Entropy:\t', MPE_ENT_PARAMS)

Multiscale Approximate Entropy:		 {}
Multiscale Sample Entropy:		 {}
Multiscale Permutation Entropy:		 {}
Multiscale WPermutation Entropy:	 {}

Calculating Multiscale Entropy Measures on Example Signals¶

# Check the calculated multsicale approximate entropy across some example signals
check_examples(examples, multi_app_entropy, MAP_ENT_PARAMS,
               'multiscale approximate entropy')

Computed multiscale approximate entropy:
  powerlaw       : 	 0.2663
  synaptic       : 	 0.3916
  knee           : 	 0.4544
  oscillation    : 	 0.0051
  burst          : 	 0.0458
  combined       : 	 0.2345
  comb_burst     : 	 0.2428
  comb_peak      : 	 0.2346

# Check the calculated multsicale sample entropy across some example signals
check_examples(examples, multi_sample_entropy, MSA_ENT_PARAMS,
               'multiscale sample entropy')

Computed multiscale sample entropy:
  powerlaw       : 	 0.4376
  synaptic       : 	 0.5150
  knee           : 	 0.6933
  oscillation    : 	 0.0055
  burst          : 	 0.0368
  combined       : 	 0.3288
  comb_burst     : 	 0.3784
  comb_peak      : 	 0.3194

# Check the calculated multsicale permutation entropy across some example signals
check_examples(examples, multi_perm_entropy, MPE_ENT_PARAMS,
               'multiscale permutation entropy')

Computed multiscale permutation entropy:
  powerlaw       : 	 0.9440
  synaptic       : 	 0.9561
  knee           : 	 0.9540
  oscillation    : 	 0.7999
  burst          : 	 0.8933
  combined       : 	 0.9451
  comb_burst     : 	 0.9449
  comb_peak      : 	 0.9464

# Check the calculated multsicale weighted permutation entropy across some example signals
check_examples(examples, multi_wperm_entropy, MWPE_ENT_PARAMS,
               'multiscale weighted permutation entropy')

Computed multiscale weighted permutation entropy:
  powerlaw       : 	 0.9041
  synaptic       : 	 0.9315
  knee           : 	 0.9150

/Users/tom/opt/anaconda3/envs/apm/lib/python3.9/site-packages/neurokit2/complexity/entropy_permutation.py:180: RuntimeWarning: invalid value encountered in divide
  freq = freq / info["Weights"].sum()

  oscillation    : 	 0.7145
  burst          : 	 0.8581
  combined       : 	 0.9062
  comb_burst     : 	 0.9080
  comb_peak      : 	 0.9153

Multiscale Approximate Entropy¶

Aperiodic Variations¶

# Run simulations calculating multiscale approximate entropy across exponents
m_ap_sims_exp = run_sims(sim_powerlaw, SIM_ITERS['ap_exp'],
                         multi_app_entropy, MAP_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale approximate entropy across exponents, with an oscillation
m_ap_sims_comb = run_sims(sim_combined, SIM_ITERS['comb_exp'],
                          multi_app_entropy, MAP_ENT_PARAMS, N_SIMS)

# Plot multiscale approximate entropy measures across aperiodic variations
plot_ap_sims(m_ap_sims_exp, m_ap_sims_comb, 'Multiscale Approximate Entropy', **fsaver('m_ap_ap'))

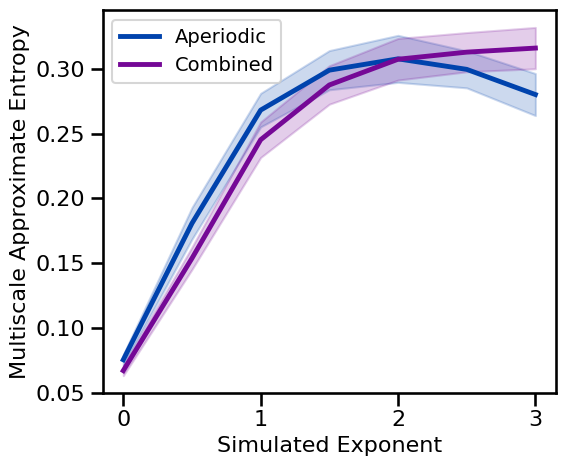
../_images/25B-Entropy-Multiscale_20_0.png

Periodic Variations¶

# Run simulations calculating multiscale approximate entropy across oscillation frequency
m_ap_sims_freq = run_sims(sim_combined, SIM_ITERS['osc_freq'],
                          multi_app_entropy, MAP_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale approximate entropy across oscillation power
m_ap_sims_pow = run_sims(sim_combined, SIM_ITERS['osc_pow'],
                         multi_app_entropy, MAP_ENT_PARAMS, N_SIMS)

# Plot multiscale approximate entropy measures across aperiodic variations
plot_pe_sims(m_ap_sims_freq, m_ap_sims_pow, 'Multiscale Approximate Entropy', **fsaver('m_ap_pe'))

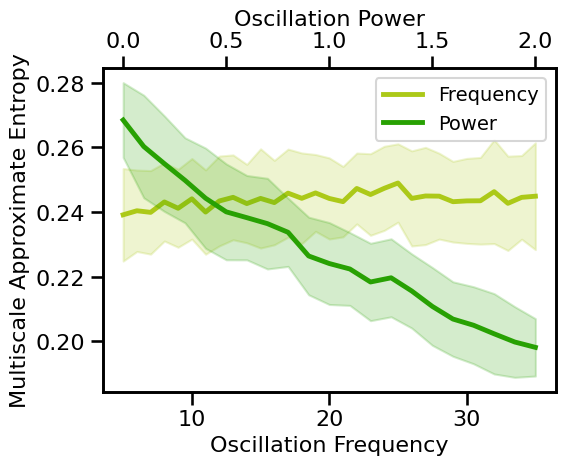
../_images/25B-Entropy-Multiscale_24_0.png

Knee Variations¶

# Run simulations calculating multiscale approximate entropy across timescales
m_ap_sims_tscales = run_sims(sim_synaptic_current, SIM_ITERS['syn_tscales'],
                             multi_app_entropy, MAP_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale approximate entropy across knee parameters
m_ap_sims_knee = run_sims_load('ap-knee-' + str(fs), multi_app_entropy, MAP_ENT_PARAMS)

# Plot the estimated multiscale approximate entropy across different timescales & knees
plot_sims_two(SIM_ITERS['syn_tscales'].values, m_ap_sims_tscales, 'Timescale',
              SIM_ITERS['kn_knee'].values, m_ap_sims_knee, 'Knee Parameter',
              ylabel='Multiscale Approximate Entropy', color=COLORS['KN'], **fsaver('m_ap_kn_vars'))

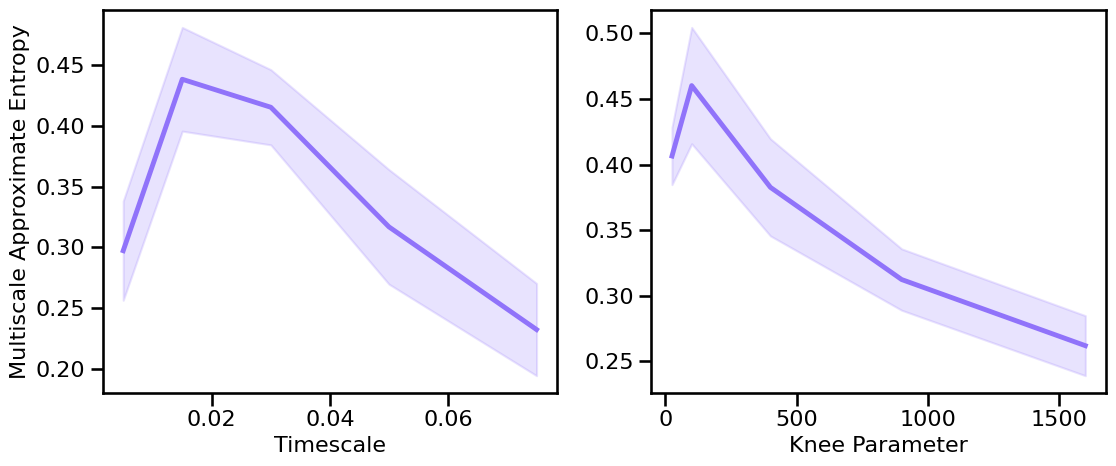
../_images/25B-Entropy-Multiscale_28_0.png

Peak Variations¶

# Run simulations calculating multiscale approximate entropy across peak bandwidths
m_ap_sims_bw = run_sims_load('comb-bw-' + str(fs), multi_app_entropy, MAP_ENT_PARAMS)

# Run simulations calculating multiscale approximate entropy across burst probabilities
m_ap_sims_burst = run_sims(sim_combined, SIM_ITERS['comb_burst'],
                           multi_app_entropy, MAP_ENT_PARAMS, N_SIMS)

# Plot the estimated multiscale approximate entropy across periodic variations
plot_sims_two(SIM_ITERS['peak_bw'].values, m_ap_sims_bw, 'Bandwidth',
              SIM_ITERS['comb_burst'].values, m_ap_sims_burst, 'Burst Probability',
              ylabel='Multiscale Approximate Entropy', color=COLORS['BW'], **fsaver('m_ap_pe_vars'))

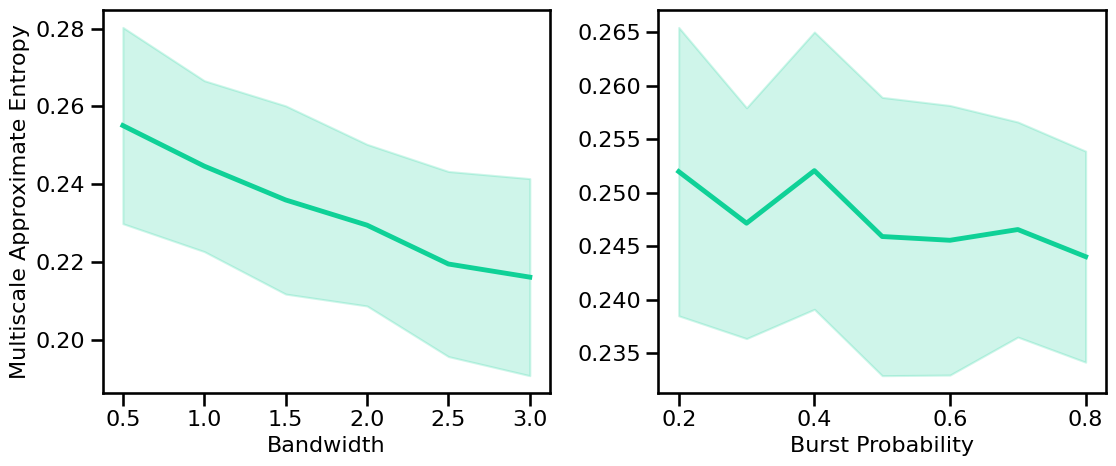
../_images/25B-Entropy-Multiscale_32_0.png

Multiscale Sample Entropy¶

Aperiodic Variations¶

# Run simulations calculating multiscale sample entropy across exponents
m_sa_sims_exp = run_sims(sim_powerlaw, SIM_ITERS['ap_exp'],
                         multi_sample_entropy, MSA_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale sample entropy across exponents, with an oscillation
m_sa_sims_comb = run_sims(sim_combined, SIM_ITERS['comb_exp'],
                          multi_sample_entropy, MSA_ENT_PARAMS, N_SIMS)

# Plot multiscale sample entropy measures across aperiodic variations
plot_ap_sims(m_sa_sims_exp, m_sa_sims_comb, 'Multiscale Sample Entropy', **fsaver('m_sa_ap'))

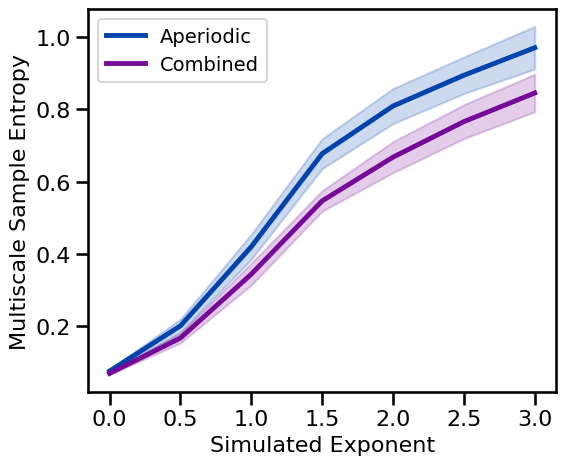
../_images/25B-Entropy-Multiscale_37_0.png

Periodic Variations¶

# Run simulations calculating multiscale sample entropy across oscillation frequency
m_sa_sims_freq = run_sims(sim_combined, SIM_ITERS['osc_freq'],
                          multi_sample_entropy, MSA_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale sample entropy across oscillation power
m_sa_sims_pow = run_sims(sim_combined, SIM_ITERS['osc_pow'],
                         multi_sample_entropy, MSA_ENT_PARAMS, N_SIMS)

# Plot multiscale approximate sample measures across aperiodic variations
plot_pe_sims(m_sa_sims_freq, m_sa_sims_pow, 'Multiscale Sample Entropy', **fsaver('m_sa_pe'))

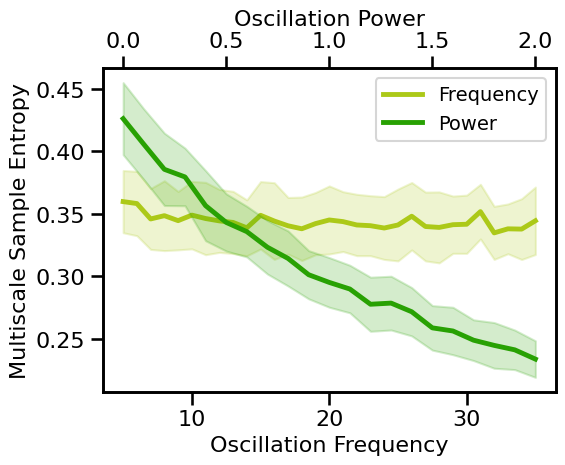
../_images/25B-Entropy-Multiscale_41_0.png

Knee Variations¶

# Run simulations calculating multiscale sample entropy across timescales
m_sa_sims_tscales = run_sims(sim_synaptic_current, SIM_ITERS['syn_tscales'],
                             multi_sample_entropy, MSA_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale sample entropy across knee parameters
m_sa_sims_knee = run_sims_load('ap-knee-' + str(fs), multi_app_entropy, MSA_ENT_PARAMS)

# Plot the estimated multiscale sample entropy across different timescales & knees
plot_sims_two(SIM_ITERS['syn_tscales'].values, m_sa_sims_tscales, 'Timescale',
              SIM_ITERS['kn_knee'].values, m_sa_sims_knee, 'Knee Parameter',
              ylabel='Multiscale Sample Entropy', color=COLORS['KN'], **fsaver('m_sa_kn_vars'))

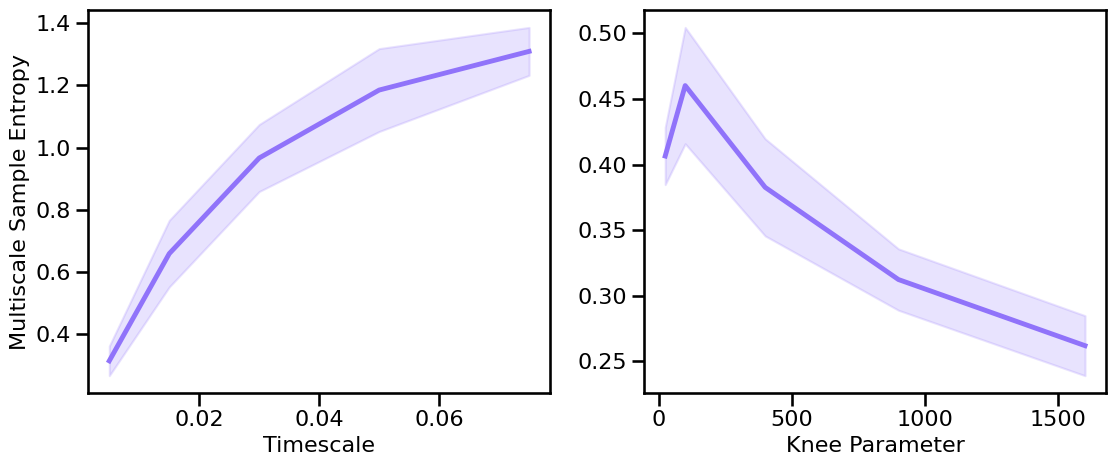
../_images/25B-Entropy-Multiscale_45_0.png

Peak Variations¶

# Run simulations calculating multiscale sample entropy across peak bandwidths
m_sa_sims_bw = run_sims_load('comb-bw-' + str(fs), multi_sample_entropy, MSA_ENT_PARAMS)

# Run simulations calculating multiscale sample entropy across burst probabilities
m_sa_sims_burst = run_sims(sim_combined, SIM_ITERS['comb_burst'],
                           multi_sample_entropy, MSA_ENT_PARAMS, N_SIMS)

# Plot the estimated multiscale approximate entropy across periodic variations
plot_sims_two(SIM_ITERS['peak_bw'].values, m_sa_sims_bw, 'Bandwidth',
              SIM_ITERS['comb_burst'].values, m_sa_sims_burst, 'Burst Probability',
              ylabel='Multiscale Sample Entropy', color=COLORS['BW'], **fsaver('m_sa_pe_vars'))

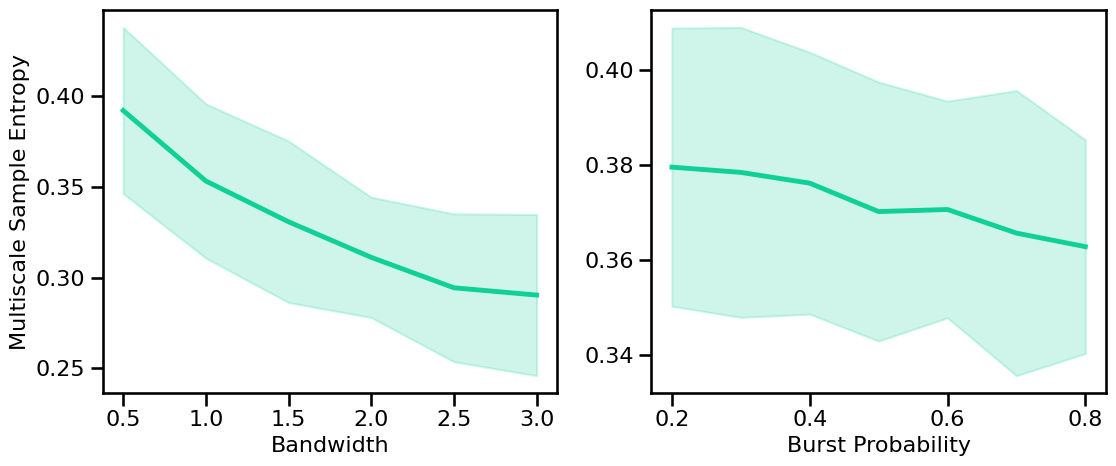
../_images/25B-Entropy-Multiscale_49_0.png

Multiscale Permutation Entropy¶

Aperiodic Variations¶

# Run simulations calculating multiscale permutation entropy across exponents
m_pe_sims_exp = run_sims(sim_powerlaw, SIM_ITERS['ap_exp'],
                         multi_perm_entropy, MPE_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale permutation entropy across exponents, with an oscillation
m_pe_sims_comb = run_sims(sim_combined, SIM_ITERS['comb_exp'],
                          multi_perm_entropy, MPE_ENT_PARAMS, N_SIMS)

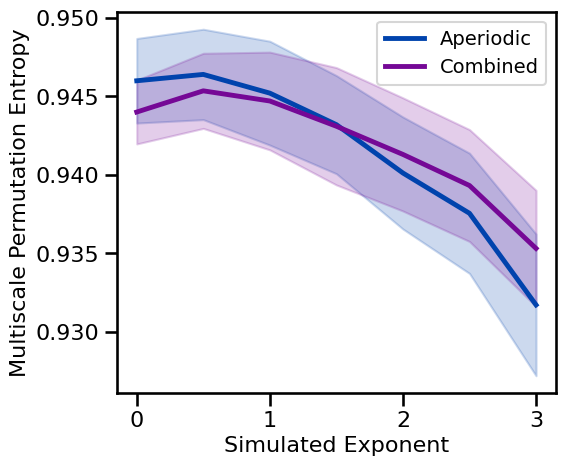
# Plot multiscale permutation entropy measures across aperiodic variations
plot_ap_sims(m_pe_sims_exp, m_pe_sims_comb, 'Multiscale Permutation Entropy', **fsaver('m_pe_ap'))

../_images/25B-Entropy-Multiscale_54_0.png

Periodic Variations¶

# Run simulations calculating multiscale permutation entropy across oscillation frequency
m_pe_sims_freq = run_sims(sim_combined, SIM_ITERS['osc_freq'],
                          multi_perm_entropy, MPE_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale permutation entropy across oscillation power
m_pe_sims_pow = run_sims(sim_combined, SIM_ITERS['osc_pow'],
                         multi_perm_entropy, MPE_ENT_PARAMS, N_SIMS)

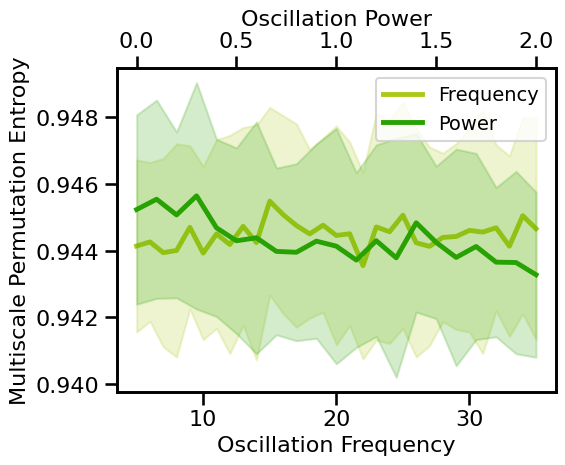
# Plot multiscale permutation entropy measures across aperiodic variations
plot_pe_sims(m_pe_sims_freq, m_pe_sims_pow, 'Multiscale Permutation Entropy', **fsaver('m_pe_pe'))

../_images/25B-Entropy-Multiscale_58_0.png

Knee Variations¶

# Run simulations calculating multiscale permutation entropy across timescales
m_pe_sims_tscales = run_sims(sim_synaptic_current, SIM_ITERS['syn_tscales'],
                             multi_perm_entropy, MPE_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale permutation entropy across knee parameters
m_pe_sims_knee = run_sims_load('ap-knee-' + str(fs), multi_perm_entropy, MPE_ENT_PARAMS)

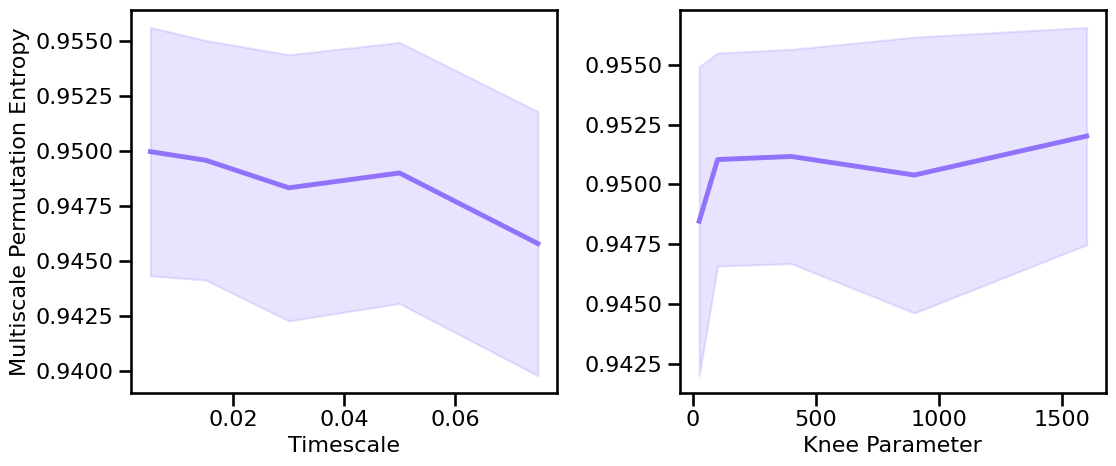
# Plot the estimated multiscale permutation entropy across different timescales & knees
plot_sims_two(SIM_ITERS['syn_tscales'].values, m_pe_sims_tscales, 'Timescale',
              SIM_ITERS['kn_knee'].values, m_pe_sims_knee, 'Knee Parameter',
              ylabel='Multiscale Permutation Entropy', color=COLORS['KN'], **fsaver('m_pe_kn_vars'))

../_images/25B-Entropy-Multiscale_62_0.png

Peak Variations¶

# Run simulations calculating multiscale permutation entropy across peak bandwidths
m_pe_sims_bw = run_sims_load('comb-bw-' + str(fs), multi_perm_entropy, MPE_ENT_PARAMS)

# Run simulations calculating multiscale permutation entropy across burst probabilities
m_pe_sims_burst = run_sims(sim_combined, SIM_ITERS['comb_burst'],
                           multi_perm_entropy, MPE_ENT_PARAMS, N_SIMS)

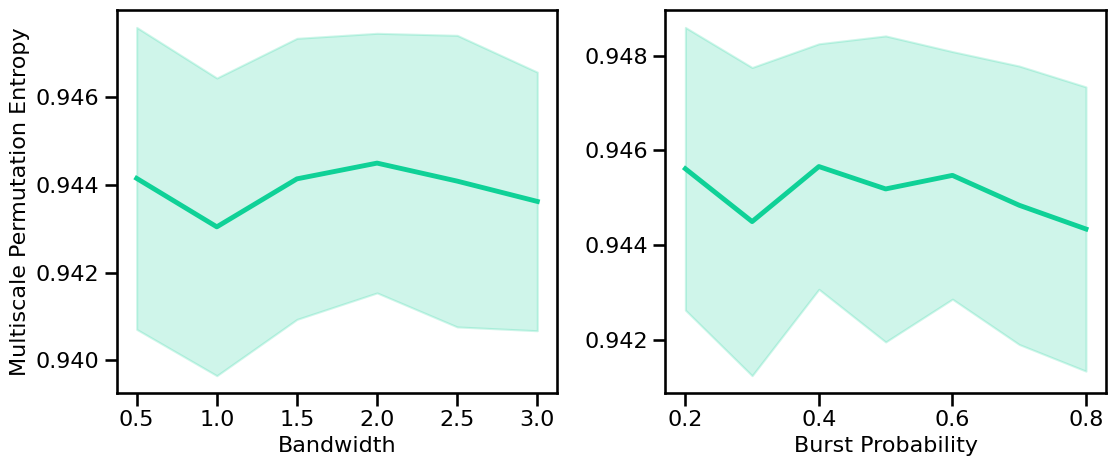
# Plot the estimated multiscale permutation entropy across periodic variations
plot_sims_two(SIM_ITERS['peak_bw'].values, m_pe_sims_bw, 'Bandwidth',
              SIM_ITERS['comb_burst'].values, m_pe_sims_burst, 'Burst Probability',
              ylabel='Multiscale Permutation Entropy', color=COLORS['BW'], **fsaver('m_pe_pe_vars'))

../_images/25B-Entropy-Multiscale_66_0.png

Multiscale Weighted Permutation Entropy¶

Aperiodic Variations¶

# Run simulations calculating multiscale weighted permutation entropy across exponents
m_wpe_sims_exp = run_sims(sim_powerlaw, SIM_ITERS['ap_exp'],
                          multi_wperm_entropy, MWPE_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale weighted permutation entropy across exponents, with an oscillation
m_wpe_sims_comb = run_sims(sim_combined, SIM_ITERS['comb_exp'],
                           multi_wperm_entropy, MWPE_ENT_PARAMS, N_SIMS)

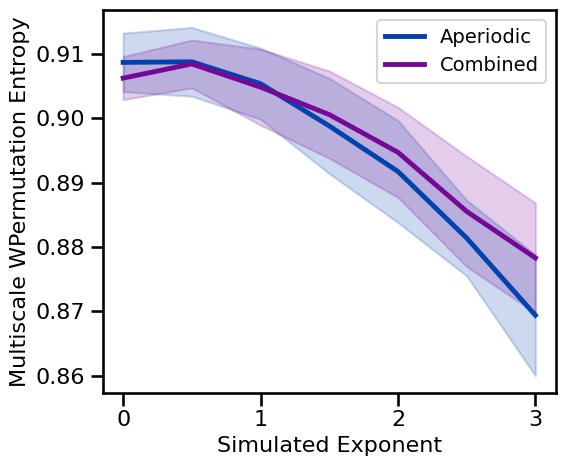
# Plot multiscale weighted permutation entropy measures across aperiodic variations
plot_ap_sims(m_wpe_sims_exp, m_wpe_sims_comb, 'Multiscale WPermutation Entropy', **fsaver('m_wpe_ap'))

../_images/25B-Entropy-Multiscale_71_0.png

Periodic Variations¶

# Run simulations calculating multiscale weighted permutation entropy across oscillation frequency
m_wpe_sims_freq = run_sims(sim_combined, SIM_ITERS['osc_freq'],
                           multi_wperm_entropy, MAP_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale weighted permutation entropy across oscillation power
m_wpe_sims_pow = run_sims(sim_combined, SIM_ITERS['osc_pow'],
                          multi_wperm_entropy, MAP_ENT_PARAMS, N_SIMS)

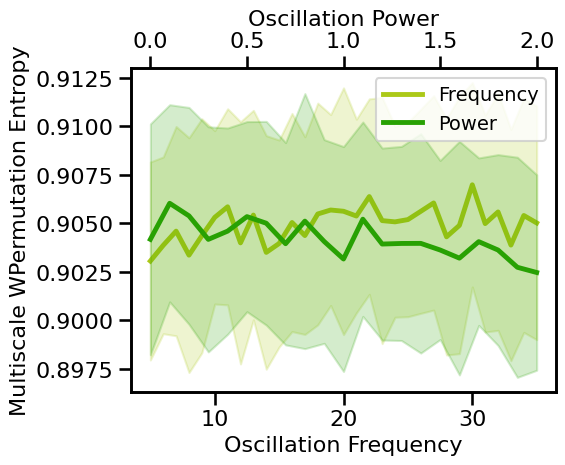
# Plot multiscale weighted permutation entropy measures across aperiodic variations
plot_pe_sims(m_wpe_sims_freq, m_wpe_sims_pow, 'Multiscale WPermutation Entropy', **fsaver('m_wpe_pe'))

../_images/25B-Entropy-Multiscale_75_0.png

Knee Variations¶

# Run simulations calculating multiscale weighted permutation entropy across timescales
m_wpe_sims_tscales = run_sims(sim_synaptic_current, SIM_ITERS['syn_tscales'],
                              multi_wperm_entropy, MWPE_ENT_PARAMS, N_SIMS)

# Run simulations calculating multiscale weighted permutation entropy across knee parameters
m_wpe_sims_knee = run_sims_load('ap-knee-' + str(fs), multi_wperm_entropy, MWPE_ENT_PARAMS)

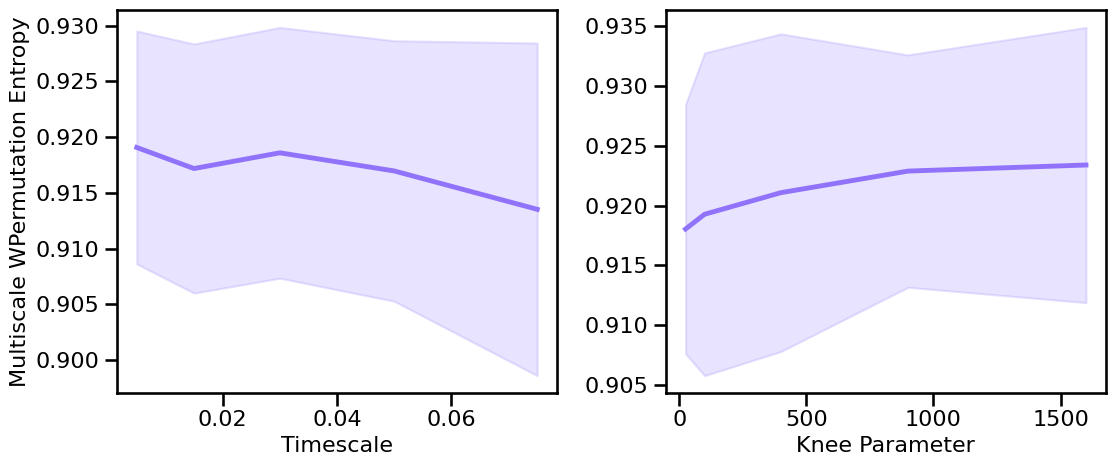
# Plot the estimated multiscale weighted permutation entropy across different timescales & knees
plot_sims_two(SIM_ITERS['syn_tscales'].values, m_wpe_sims_tscales, 'Timescale',
              SIM_ITERS['kn_knee'].values, m_wpe_sims_knee, 'Knee Parameter',
              ylabel='Multiscale WPermutation Entropy', color=COLORS['KN'], **fsaver('m_wpe_kn_vars'))

../_images/25B-Entropy-Multiscale_79_0.png

Peak Variations¶

# Run simulations calculating multiscale weighted permutation entropy across peak bandwidths
m_wpe_sims_bw = run_sims_load('comb-bw-' + str(fs), multi_wperm_entropy, MWPE_ENT_PARAMS)

# Run simulations calculating multiscale weighted permutation entropy across burst probabilities
m_wpe_sims_burst = run_sims(sim_combined, SIM_ITERS['comb_burst'],
                            multi_wperm_entropy, MWPE_ENT_PARAMS, N_SIMS)

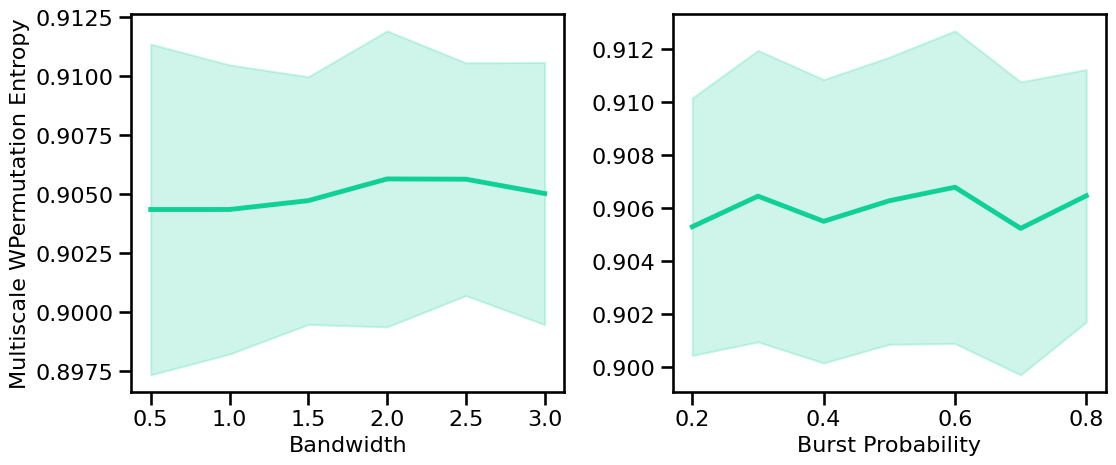
# Plot the estimated multiscale permutation entropy across periodic variations
plot_sims_two(SIM_ITERS['peak_bw'].values, m_wpe_sims_bw, 'Bandwidth',
              SIM_ITERS['comb_burst'].values, m_wpe_sims_burst, 'Burst Probability',
              ylabel='Multiscale WPermutation Entropy', color=COLORS['BW'],  **fsaver('m_wpe_pe_vars'))

../_images/25B-Entropy-Multiscale_83_0.png

Conclusions¶

From these simulations we can see that:

for multiscale approximate and sample entropy, measures tend to increase with increasing aperiodic exponent
for multiscale permutation and weighted permutation entropy, measures tend to decrease with increasing aperiodic exponent
estimates of multiscale entropy tend to be quite stable across variations of oscillation frequency and power

Aperiodic Methods

Multiscale Entropy

Contents

Multiscale Entropy¶

Settings¶

Multiscale Entropy¶

Calculating Multiscale Entropy Measures on Example Signals¶

Multiscale Approximate Entropy¶

Aperiodic Variations¶

Periodic Variations¶

Knee Variations¶

Peak Variations¶

Multiscale Sample Entropy¶

Aperiodic Variations¶

Periodic Variations¶

Knee Variations¶

Peak Variations¶

Multiscale Permutation Entropy¶

Aperiodic Variations¶

Periodic Variations¶

Knee Variations¶

Peak Variations¶

Multiscale Weighted Permutation Entropy¶

Aperiodic Variations¶

Periodic Variations¶

Knee Variations¶

Peak Variations¶

Conclusions¶