Developmental EEG Data
Contents
Developmental EEG Data¶
This notebook analyzes a large dataset of EEG, collected from a developmental sample.
Dataset Details¶
This analysis uses the MIPDB dataset from the ChildMind Institute.
Note that the pre-processing of the data as available in the dataset, doing data cleaning and calculating power spectra, is done external to this project.
# Setup notebook state
from nbutils import setup_notebook; setup_notebook()
import numpy as np
import matplotlib.pyplot as plt
from fooof import FOOOFGroup
from fooof.utils import trim_spectrum
from fooof.objs import combine_fooofs
from neurodsp.utils import create_times
from neurodsp.spectral import compute_spectrum
from neurodsp.plts import plot_time_series, plot_power_spectra
from neurodsp.plts.utils import make_axes
from bootstrap import bootstrap_diff
# Import custom project code
from apm.io import APMDB, get_files, load_pickle
from apm.io.data import load_eeg_dev_info
from apm.analysis import compute_avgs
from apm.analysis.corrs import (compute_all_corrs, compute_corrs_to_feature,
unpack_corrs, compute_reg_var)
from apm.plts import plot_dots, plot_corr_matrix
from apm.plts.results import plot_topo
from apm.plts.multi import plot_results_all, plot_topo_row
from apm.plts.utils import figsaver, plot_colorbar
from apm.plts.settings import LABELS
from apm.utils import format_corr
# Import dataset settings from script
import sys; from pathlib import Path;
sys.path.append(str(Path('..').resolve() / 'scripts'))
from scripts.analyze_eeg2 import DATA_FOLDER, FS
Set Up Paths¶
# Define load path
db = APMDB()
LOADPATH = db.data_path / 'eeg2'
# Check the set of results files available for this dataset
get_files(LOADPATH)
['eeg2_results.p',
'eeg2_results_peaks.p',
'eeg2_spatial_alpha_corrs.p',
'eeg2_spatial_alpha_corrs_diffs.p',
'eeg2_spatial_corrs.p',
'eeg2_spatial_exp_corrs.p',
'specparam',
'zOLD']
Settings¶
# Set time of loaded data
n_seconds = 30
# Define times vector for data
times = create_times(n_seconds + 1 / FS, FS)
# Add plot kwargs
dot_kwargs = {
's' : 24,
'alpha' : 0.7,
}
# Settings for saving figures
SAVE_FIG = True
FIGPATH = db.figs_path / '52_dev_data'
# Create helper function to manage figsaver settings
fsaver = figsaver(SAVE_FIG, FIGPATH)
# Define topography vlims for each measure
vlims = {
'autocorr_decay_time' : (0.01, 0.12),
'dfa' : (0.75, 1.25),
'higuchi_fd' : (1.4, 1.75),
'hjorth_complexity' : (4.5, 5.75),
'lempelziv' : (375, 450),
'sample_entropy' : (0.75, 1.05),
'perm_entropy' : (2.4, 2.55),
'irasa' : (1.5, 1.95),
'specparam' : (1.5, 1.95),
}
Load Data¶
# Load group data
group_data = np.load(DATA_FOLDER / 'MIPDB_extracted_block.npy')
# Check the size of the dataset
n_subjs, n_blocks, n_chs, n_times = group_data.shape
print('# of subjects: \t', n_subjs)
print('# of blocks: \t', n_blocks)
print('# of channels: \t', n_chs)
# of subjects: 111
# of blocks: 5
# of channels: 111
# Load metadata
ages = np.load(DATA_FOLDER / 'ages.npy')
# Sub-select the first block of data
group_data = np.squeeze(group_data[:, 0, :, :])
# Load MNE info object for the current dataset
info = load_eeg_dev_info(DATA_FOLDER)
Data Checks¶
# Set example subject index
subj_ind = 2
# Set example channel index
chi = 110
# Check example channel label
info.ch_names[chi]
'Cz'
# Plot a segment of time series data
plot_time_series(times, group_data[subj_ind, chi], xlim=[5, 10], lw=1., figsize=(12, 1))
plt.gca().axis('off');
if SAVE_FIG: plt.savefig(FIGPATH / ('eeg2_timeseries.pdf'))

# Compute a power spectrum of an example
freqs, powers = compute_spectrum(group_data[subj_ind, chi], FS, nperseg=2*FS, noverlap=FS)
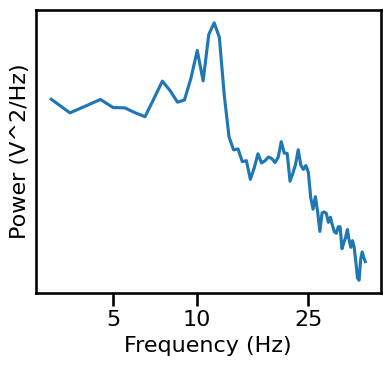
# Plot power spectrum of example signal
plot_power_spectra(*trim_spectrum(freqs, powers, [3, 40]), minorticks=False,
xticks=[5, 10, 25], xticklabels=[5, 10, 25], yticks=[],
figsize=(4.25, 4), **fsaver('eeg2_psd'))
Check Spectral Fits¶
# Load specparam measures
all_fgs = []
temp = FOOOFGroup()
for fres in get_files(LOADPATH / 'specparam'):
temp.load(fres, LOADPATH / 'specparam')
all_fgs.append(temp.copy())
fg = combine_fooofs(all_fgs)
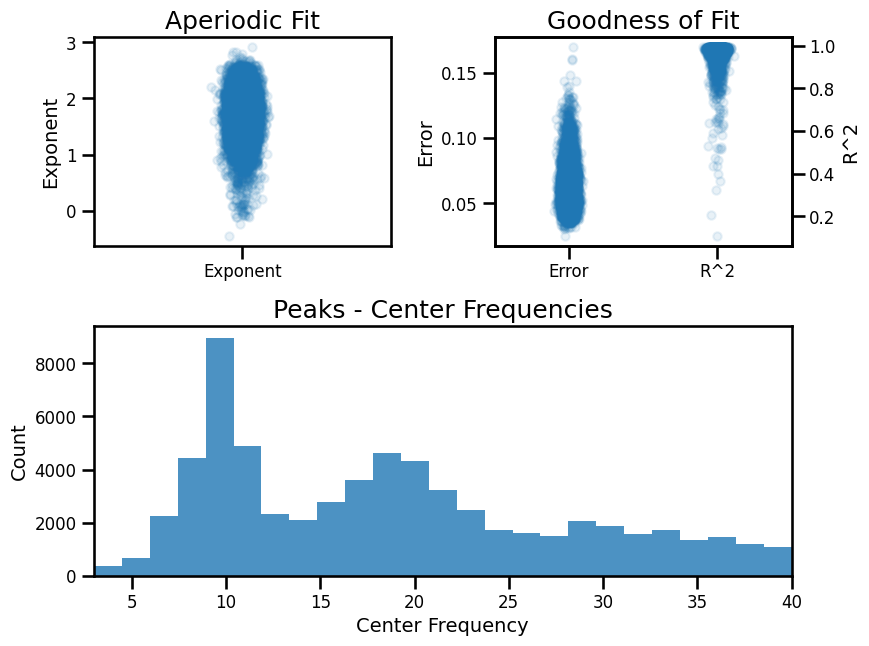
# Check overall group results
fg.print_results()
fg.plot()
==================================================================================================
FOOOF - GROUP RESULTS
Number of power spectra in the Group: 12321
The model was run on the frequency range 3 - 40 Hz
Frequency Resolution is 0.50 Hz
Power spectra were fit without a knee.
Aperiodic Fit Values:
Exponents - Min: -0.449, Max: 2.924, Mean: 1.685
In total 64398 peaks were extracted from the group
Goodness of fit metrics:
R2s - Min: 0.107, Max: 0.996, Mean: 0.977
Errors - Min: 0.025, Max: 0.170, Mean: 0.061
==================================================================================================
Load Results¶
# Load precomputed group results
group_results = load_pickle('eeg2_results', LOADPATH)
# Check size of computed results [n_subjs, n_chs]
group_results['dfa'].shape
(111, 111)
# Load precomputed peak results
group_results_peaks = load_pickle('eeg2_results_peaks', LOADPATH)
Check Measures & Labels¶
# Check list of computed measures
print(list(group_results.keys()))
['autocorr_decay_time', 'dfa', 'higuchi_fd', 'hjorth_complexity', 'lempelziv', 'sample_entropy', 'perm_entropy', 'irasa', 'specparam']
# Collect list of exponent & timeseries measure labels
exp_measures = ['specparam', 'irasa']
ts_measures = list(group_results.keys())
[ts_measures.remove(meas) for meas in exp_measures];
# Collect labels for time series measures
ts_labels = [LABELS[meas] for meas in ts_measures]
Extract Measures for Example Channel¶
# Sub-select results to channel of interest
results = {key : val[:, chi] for key, val in group_results.items()}
results_peaks = {key : val[:, chi] for key, val in group_results_peaks.items()}
# Compute correlations for selected channel
all_corrs = compute_all_corrs(results)
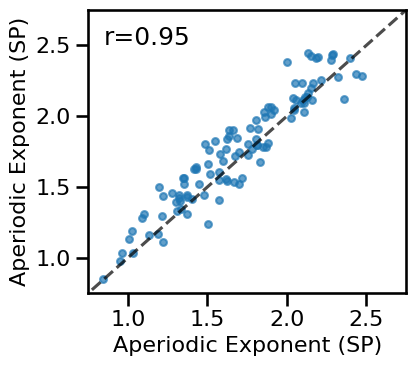
Compare Exponent Measures¶
# Plot the comparison of specparam and IRASA exponent estimations
plot_dots(results['specparam'], results['irasa'], **dot_kwargs, figsize=(4.5, 4),
xlim=[0.75, 2.75], ylim=[0.75, 2.75], tposition='tl', expected=[0, 3],
xlabel='Aperiodic Exponent (SP)', ylabel='Aperiodic Exponent (SP)',
**fsaver('eeg2_exp_exp_comp'))
# Check correlation between specparam and irasa exponent estimates
print(' SP-EXP & IR-EXP: ', format_corr(*all_corrs['specparam']['irasa']))
SP-EXP & IR-EXP: r=+0.950 CI[+0.919, +0.965], p=0.000
Compare Exponent to Time Series Measures¶
# Plot comparisons between exponent and time series measures
axes = make_axes(1, len(ts_measures), figsize=(26, 4), wspace=0.1)
for ind, meas in enumerate(ts_measures):
plot_dots(results['specparam'], results[meas],
**dot_kwargs, tposition='tr' if not ind == 6 else 'br',
xlabel='Aperiodic Exponent', ylabel=LABELS[meas], ax=axes[ind])
if SAVE_FIG: plt.savefig(FIGPATH / ('exp_ts_scatters.pdf'))

# Check the correlations between time series and exponent measures
for meas in ts_measures:
print(meas)
print(' SP-EXP: ', format_corr(*all_corrs['specparam'][meas]))
print(' IR-EXP: ', format_corr(*all_corrs['irasa'][meas]))
autocorr_decay_time
SP-EXP: r=+0.032 CI[-0.176, +0.232], p=0.741
IR-EXP: r=-0.075 CI[-0.280, +0.136], p=0.434
dfa
SP-EXP: r=-0.405 CI[-0.551, -0.241], p=0.000
IR-EXP: r=-0.493 CI[-0.631, -0.338], p=0.000
higuchi_fd
SP-EXP: r=-0.407 CI[-0.556, -0.227], p=0.000
IR-EXP: r=-0.486 CI[-0.632, -0.311], p=0.000
hjorth_complexity
SP-EXP: r=+0.461 CI[+0.292, +0.599], p=0.000
IR-EXP: r=+0.467 CI[+0.309, +0.603], p=0.000
lempelziv
SP-EXP: r=-0.413 CI[-0.561, -0.240], p=0.000
IR-EXP: r=-0.409 CI[-0.555, -0.248], p=0.000
sample_entropy
SP-EXP: r=-0.423 CI[-0.560, -0.258], p=0.000
IR-EXP: r=-0.430 CI[-0.563, -0.272], p=0.000
perm_entropy
SP-EXP: r=-0.073 CI[-0.258, +0.113], p=0.445
IR-EXP: r=-0.099 CI[-0.281, +0.092], p=0.301
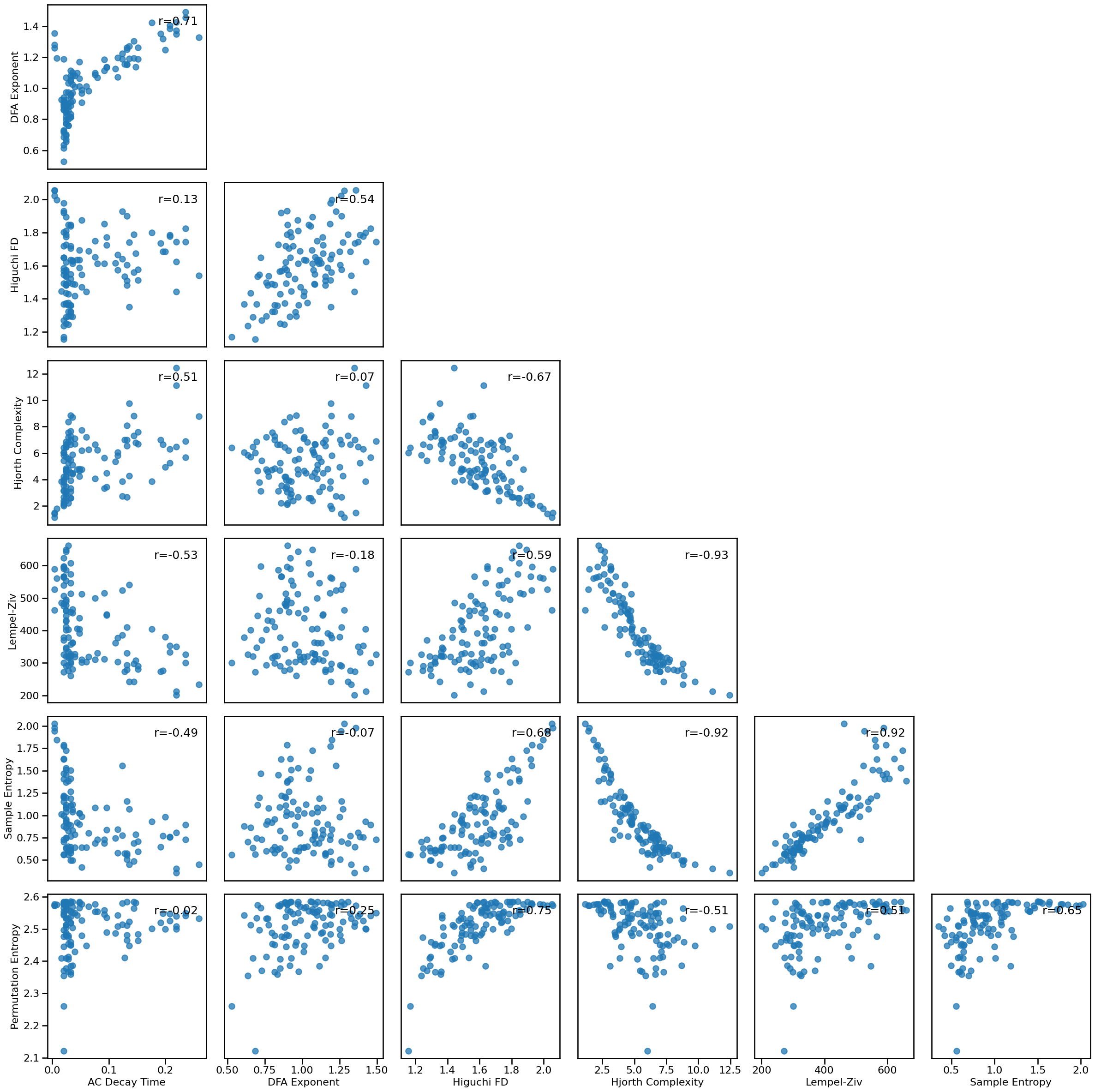
Compare Time Series Measures to Each Other¶
# Plot multi-panel plot comparing all time series measures to each other
plot_results_all(results, ts_measures)
Correlations¶
# Subselect time domain measures
all_corrs_ts = {ke : va for ke, va in all_corrs.items() if ke not in exp_measures}
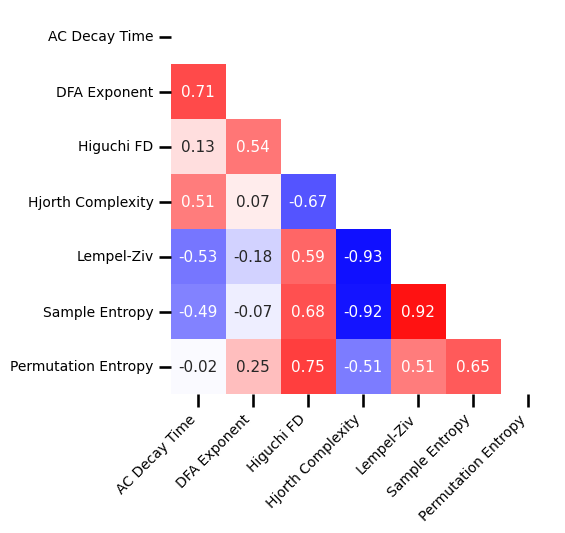
# Plot correlation matrix between time series measures
plot_corr_matrix(unpack_corrs(all_corrs_ts), cbar=False, figsize=(5, 5),
xticklabels=ts_labels, yticklabels=ts_labels, **fsaver('subj_corrs_ts'))
# Extract the correlations between specparam and time domain measures
exp_corrs_subjs = np.atleast_2d([all_corrs['specparam'][label][0] for label in ts_measures]).T
# Plot correlation of time series measures to exponent
plot_corr_matrix(exp_corrs_subjs, cbar=False, figsize=(1.5, 5), **fsaver('subj_corrs_exp'))

Compare to Alpha Power¶
# Compute correlations between aperiodic measures and alpha power
alpha_corrs = compute_corrs_to_feature(results, results_peaks['alpha_power'])
# # Compute differences between correlations to alpha
# alpha_corr_diffs = compute_diffs_to_feature(results, results_peaks['alpha_power'])
# Check the correlations between alpha power and aperiodic measures
print('Correlations with alpha:')
for label in alpha_corrs.keys():
print(' {:20s}: '.format(label), format_corr(*alpha_corrs[label]))
Correlations with alpha:
autocorr_decay_time : r=-0.189 CI[-0.381, +0.018], p=0.046
dfa : r=-0.484 CI[-0.621, -0.328], p=0.000
higuchi_fd : r=-0.609 CI[-0.715, -0.476], p=0.000
hjorth_complexity : r=+0.279 CI[+0.104, +0.440], p=0.003
lempelziv : r=-0.262 CI[-0.426, -0.084], p=0.005
sample_entropy : r=-0.370 CI[-0.517, -0.203], p=0.000
perm_entropy : r=-0.487 CI[-0.618, -0.322], p=0.000
irasa : r=+0.418 CI[+0.243, +0.564], p=0.000
specparam : r=+0.314 CI[+0.140, +0.476], p=0.001
# Organize correlations between alpha and time domain measures
alpha_corrs_ts = np.atleast_2d([alpha_corrs[label][0] for label in ts_measures]).T
# Plot correlations between alpha and time domain measures
plot_corr_matrix(alpha_corrs_ts, cbar=False, figsize=(1.5, 5), **fsaver('subj_corrs_alpha'))

Check Age Relationship¶
# Compute the correlations between each measure and age
age_corrs = compute_corrs_to_feature(results, ages)
# # Compute the differences between measure-to-age correlations
# age_corr_diffs = compute_diffs_to_feature(results, ages)
Check Correlations with Age¶
# Check the correlations between age and aperiodic measures
print('Correlations with age:')
for label in age_corrs.keys():
print(' {:20s}: '.format(label), format_corr(*age_corrs[label]))
Correlations with age:
autocorr_decay_time : r=-0.146 CI[-0.330, +0.039], p=0.125
dfa : r=+0.127 CI[-0.051, +0.298], p=0.184
higuchi_fd : r=+0.157 CI[-0.027, +0.323], p=0.101
hjorth_complexity : r=-0.218 CI[-0.392, -0.033], p=0.021
lempelziv : r=+0.213 CI[+0.028, +0.381], p=0.025
sample_entropy : r=+0.297 CI[+0.121, +0.453], p=0.002
perm_entropy : r=+0.194 CI[+0.015, +0.371], p=0.042
irasa : r=-0.469 CI[-0.597, -0.318], p=0.000
specparam : r=-0.519 CI[-0.635, -0.381], p=0.000
Exponent - Age Relationships¶
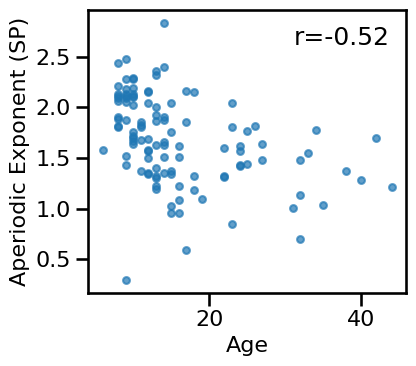
# Plot the relationship between exponent (SP) and age
plot_dots(ages, results['specparam'], **dot_kwargs, figsize=(4.5, 4),
xlabel='Age', ylabel='Aperiodic Exponent (SP)', **fsaver('eeg2_exp_sp_age_corr'))
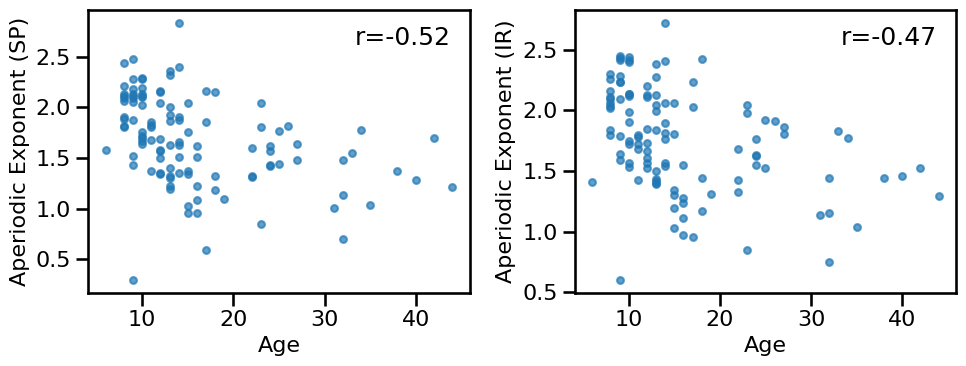
# Check the relationship between aperiodic exponent and age
axes = make_axes(1, 2, figsize=(10, 4), wspace=0.25)
plot_dots(ages, results['specparam'], **dot_kwargs, ax=axes[0],
xlabel='Age', ylabel='Aperiodic Exponent (SP)')
plot_dots(ages, results['irasa'], **dot_kwargs, ax=axes[1],
xlabel='Age', ylabel='Aperiodic Exponent (IR)')
if SAVE_FIG: plt.savefig(FIGPATH / ('mipdb_exp_age.pdf'))
Time Domain - Age Relationships¶
# Check the relationship between time domain measures and age
axes = make_axes(1, len(ts_measures), figsize=(30, 4), wspace=0.05)
for ind, meas in enumerate(ts_measures):
plot_dots(ages, results[meas], **dot_kwargs, tposition='tr' if not ind == 6 else 'br',
xlabel='Age', ylabel=LABELS[meas], ax=axes[ind])
if SAVE_FIG: plt.savefig(FIGPATH / ('eeg2_ts_age.pdf'))

Partial Age Correlations¶
# Compute residualized versions of measures (remove specparam)
results_res = {meas : compute_reg_var(results[meas], results['specparam']) for meas in ts_measures}
# Compute the correlations between each measure and age
age_corrs_res = compute_corrs_to_feature(results_res, ages)
# Check the correlations between age and partialed aperiodic measures
print('Correlations with age:')
for label in age_corrs_res.keys():
print(' {:20s}: '.format(label), format_corr(*age_corrs_res[label]))
Correlations with age:
autocorr_decay_time : r=-0.257 CI[-0.439, -0.068], p=0.006
dfa : r=-0.069 CI[-0.243, +0.109], p=0.470
higuchi_fd : r=-0.017 CI[-0.196, +0.170], p=0.860
hjorth_complexity : r=-0.035 CI[-0.229, +0.160], p=0.712
lempelziv : r=+0.022 CI[-0.161, +0.205], p=0.818
sample_entropy : r=+0.087 CI[-0.102, +0.270], p=0.364
perm_entropy : r=+0.135 CI[-0.048, +0.312], p=0.159
# Check the relationship between time domain measures and age
axes = make_axes(1, len(ts_measures), figsize=(30, 4), wspace=0.05)
for ind, meas in enumerate(ts_measures):
plot_dots(ages, results_res[meas],
**dot_kwargs, tposition='tr' if not ind == 6 else 'br',
xlabel='Age', ylabel=LABELS[meas], ax=axes[ind])
if SAVE_FIG: plt.savefig(FIGPATH / ('eeg2_ts_age_partial.pdf'))

# Compute the bootstrapped difference tests between correlations
print('Partial correlations differences:')
for label in ts_measures:
print(' {:20s}: '.format(label),
format_corr(*bootstrap_diff(ages, results[label], results_res[label])))
Partial correlations differences:
autocorr_decay_time : r=+0.111 CI[+0.046, +0.186], p=0.000
dfa : r=+0.196 CI[+0.113, +0.275], p=0.000
higuchi_fd : r=+0.173 CI[+0.099, +0.246], p=0.000
hjorth_complexity : r=-0.183 CI[-0.262, -0.099], p=0.000
lempelziv : r=+0.191 CI[+0.113, +0.272], p=0.000
sample_entropy : r=+0.210 CI[+0.117, +0.303], p=0.000
perm_entropy : r=+0.059 CI[+0.031, +0.090], p=0.000
Spatial Analyses¶
Compute Measures Across Channels¶
# Compute the group average topographies
group_avg = compute_avgs(group_results)
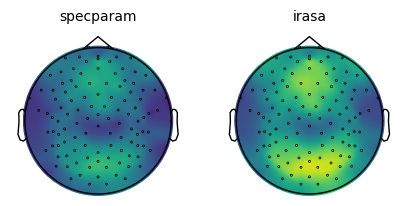
Exponent Topographies¶
# Plot the group average topographies for the exponent measures
plot_topo_row(group_avg, exp_measures, info, vlims=vlims, wspace=0.2, **fsaver('exp_topos'))
# Create colorbar for the aperiodic exponent topographies
plot_colorbar('Aperiodic Exponent', *vlims['specparam'],
**fsaver('colorbar_eeg2_exp'), close=True)
# Compute correlation between exponent topographies
exp_spatial_corr = compute_all_corrs({meas: group_avg[meas] for meas in exp_measures})
# Check correlation between specparam and irasa exponent estimates
print(' SP-EXP & IR-EXP: ', format_corr(*exp_spatial_corr['specparam']['irasa']))
SP-EXP & IR-EXP: r=+0.973 CI[+0.955, +0.981], p=0.000
Time Series Measure Topographies¶
# Plot the group average topographies for the time domain measures
plot_topo_row(group_avg, ts_measures, info, vlims=vlims, wspace=0.25)

Spatial Correlations¶
# Load precomputed group correlation results
group_corrs = load_pickle('eeg2_spatial_corrs', LOADPATH)
# Unpack correlations for plotting
group_corrs_mat = unpack_corrs(group_corrs)
# Unpack correlations for plotting, and compute mask
mask = np.triu(group_corrs_mat)
labels = list(group_corrs.keys())
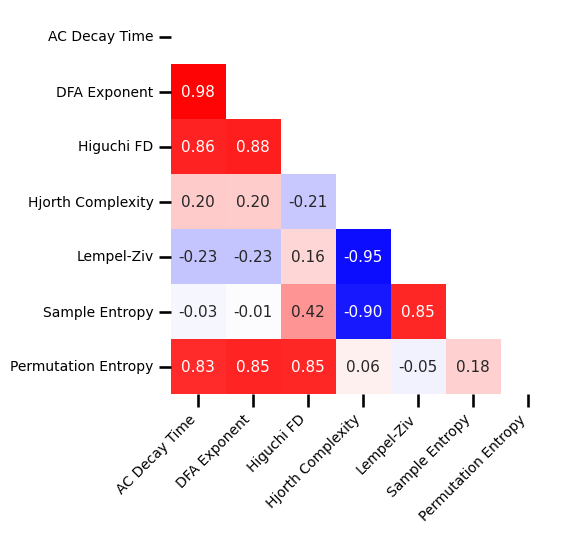
# Plot the correlation matrix of spatial topographies
plot_corr_matrix(group_corrs_mat, cbar=False, figsize=(5, 5),
xticklabels=ts_labels, yticklabels=ts_labels, **fsaver('spatial_corrs_ts'))
# Load precomputed group exponent correlation results
group_exp_corrs = load_pickle('eeg2_spatial_exp_corrs', LOADPATH)
# Organize the correlations between the exponent and time domain measures
exp_corr_mat = np.atleast_2d([group_exp_corrs[label][0] for label in group_exp_corrs]).T
# Plot the correlations between exponent and time domain measures
plot_corr_matrix(exp_corr_mat, cbar=False, figsize=(1.5, 5), **fsaver('spatial_corrs_exp'))

Alpha Power Topography¶
# Compute the average alpha topography across the group
group_avg_peaks = compute_avgs(group_results_peaks)
# Check range of alpha power values
amin, amax = np.min(group_avg_peaks['alpha_power']), np.max(group_avg_peaks['alpha_power'])
amin, amax
(-0.2274266529501394, 0.8801155434513204)
# Set alpha vlimits
alpha_vlim = (-0.20, 0.90)
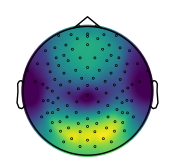
# Plot the average alpha topography across the group
plot_topo(group_avg_peaks['alpha_power'], info, vlim=alpha_vlim)
# Create colorbar for the aperiodic exponent topographies
plot_colorbar('Alpha Power (uV**2)', *alpha_vlim, figsize=(2.65, 7),
**fsaver('colorbar_eeg1_alpha'), close=True)
# Load precomputed correlations between aperiodic measures and alpha power
group_alpha_corrs = load_pickle('eeg2_spatial_alpha_corrs', LOADPATH)
# # Load precomputed differences between correlations between aperiodic measures and alpha power
# group_alpha_corr_diffs = load_pickle('eeg2_spatial_alpha_corr_diffs', LOADPATH)
# Organize the alpha correlations
alpha_corr_mat = np.atleast_2d([group_alpha_corrs[label][0] for label in group_alpha_corrs]).T
# Plot the correlations between alpha activity and time domain measures
plot_corr_matrix(alpha_corr_mat, cbar=False, figsize=(1.5, 5), **fsaver('spatial_corrs_alpha'))

Conclusions¶
Interim conclusions from this analysis:
specparam & IRASA estimates are consistent in this dataset
aperiodic exponent is moderately correlated with time domain measures
Notably, these findings are a replication of the same analyses on the previous EEG dataset.
In addition, in this larger dataset, we could analyze the relationship between our measures of interest, and age, finding that:
specparam & IRASA estimates of exponent are equivalently correlated with age
time domain measures are more moderately correlated with age than exponent measures