Information Metrics
Contents
Information Metrics¶
This notebooks runs information theory metrics on time series signals, including several entropy measures.
This notebook includes:
approximate entropy
sample entropy
permutation entropy
weighted permutation entropy
# Setup notebook state
from nbutils import setup_notebook; setup_notebook()
from neurodsp.sim import sim_powerlaw, sim_synaptic_current, sim_combined
from neurodsp.utils import set_random_seed
# Import custom project code
from apm.io import APMDB
from apm.run import run_sims_load
from apm.run import run_sims_parallel as run_sims
from apm.methods import app_entropy, sample_entropy, perm_entropy, wperm_entropy
from apm.methods.settings import (AP_ENT_PARAMS, SA_ENT_PARAMS,
PE_ENT_PARAMS, WPE_ENT_PARAMS)
from apm.plts.sims import plot_ap_sims, plot_pe_sims, plot_sims_two
from apm.plts.settings import COLORS
from apm.plts.utils import figsaver
from apm.sim.examples import get_examples, check_examples
from apm.sim.settings import N_SIMS
from apm.sim.defs import SIM_ITERS
Settings¶
# Get current sampling rate
fs = SIM_ITERS.fs
# Settings for saving figures
SAVE_FIG = True
FIGPATH = APMDB().figs_path / '25_entropy'
# Create helper function to manage figsaver settings
fsaver = figsaver(SAVE_FIG, FIGPATH)
# Set the random seed
set_random_seed(111)
# Define collection of example signals
examples = get_examples()
Entropy Measures¶
# Check settings for entropy measures
print('Approximate Entropy:\t', AP_ENT_PARAMS)
print('Sample Entropy: \t', SA_ENT_PARAMS)
print('Permutation Entropy:\t', PE_ENT_PARAMS)
print('WPermutation Entropy:\t', WPE_ENT_PARAMS)
Approximate Entropy: {'order': 2}
Sample Entropy: {'order': 2}
Permutation Entropy: {'order': 3, 'delay': 1}
WPermutation Entropy: {'order': 3, 'delay': 1}
Calculating Entropy Measures on Example Signals¶
Entropy measures generally measure the level of ‘randomness’ or complexity in a signal.
In all cases, smaller values of measured entropy indicate more regular time series.
# Check the calculated approximate entropy across some example signals
check_examples(examples, app_entropy, AP_ENT_PARAMS, 'approximate entropy')
Computed approximate entropy:
powerlaw : 1.9050
synaptic : 1.9387
knee : 1.6985
oscillation : 0.1842
burst : 0.1081
combined : 1.7746
comb_burst : 1.8253
comb_peak : 1.7808
# Check the calculated sample entropy across some example signals
check_examples(examples, sample_entropy, SA_ENT_PARAMS, 'sample entropy')
Computed sample entropy:
powerlaw : 1.8611
synaptic : 1.9033
knee : 1.6268
oscillation : 0.2815
burst : 0.0267
combined : 1.7109
comb_burst : 1.7600
comb_peak : 1.7061
# Check the calculated permutation entropy across some example signals
check_examples(examples, perm_entropy, PE_ENT_PARAMS, 'permutation entropy')
Computed permutation entropy:
powerlaw : 2.5664
synaptic : 2.5496
knee : 2.4861
oscillation : 1.4010
burst : 1.1077
combined : 2.5515
comb_burst : 2.5549
comb_peak : 2.5551
# Check the calculated weighted permutation entropy across some example signals
check_examples(examples, wperm_entropy, WPE_ENT_PARAMS, 'weighted permutation entropy')
Computed weighted permutation entropy:
powerlaw : 0.9634
synaptic : 0.9404
knee : 0.8551
oscillation : 0.3930
burst : 0.4080
combined : 0.9552
comb_burst : 0.9609
comb_peak : 0.9542
Approximate Entropy¶
Approximate entropy quantifies the unpredictability of a time series.
Aperiodic Variations¶
# Run simulations calculating approximate entropy across exponents
ap_sims_exp = run_sims(sim_powerlaw, SIM_ITERS['ap_exp'], app_entropy, AP_ENT_PARAMS, N_SIMS)
# Run simulations calculating approximate entropy across exponents, with an oscillation
ap_sims_comb = run_sims(sim_combined, SIM_ITERS['comb_exp'], app_entropy, AP_ENT_PARAMS, N_SIMS)
# Plot approximate entropy measures across aperiodic variations
plot_ap_sims(ap_sims_exp, ap_sims_comb, 'Approximate Entropy', **fsaver('ap_ap'))
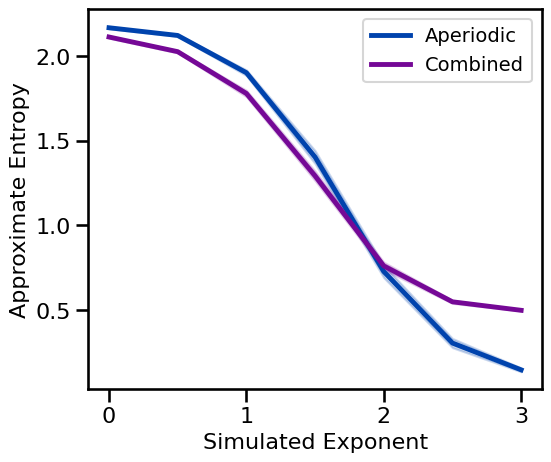
Periodic Variations¶
# Run simulations calculating approximate entropy across oscillation frequency
ap_sims_freq = run_sims(sim_combined, SIM_ITERS['osc_freq'], app_entropy, AP_ENT_PARAMS, N_SIMS)
# Run simulations calculating approximate entropy across oscillation power
ap_sims_pow = run_sims(sim_combined, SIM_ITERS['osc_pow'], app_entropy, AP_ENT_PARAMS, N_SIMS)
# Plot approximate entropy measures across aperiodic variations
plot_pe_sims(ap_sims_freq, ap_sims_pow, 'Approximate Entropy', **fsaver('ap_pe'))
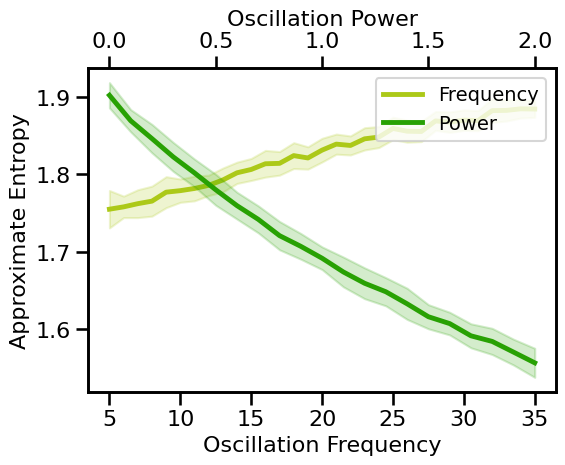
Knee Variations¶
# Run simulations calculating approximate entropy across timescales
ap_sims_tscales = run_sims(sim_synaptic_current, SIM_ITERS['syn_tscales'],
app_entropy, AP_ENT_PARAMS, N_SIMS)
# Run simulations calculating approximate exntropy across different knee parameters (sims from file)
ap_sims_knee = run_sims_load('ap-knee-' + str(fs), app_entropy, AP_ENT_PARAMS)
# Plot the estimated approximate entropy across different timescales & knees
plot_sims_two(SIM_ITERS['syn_tscales'].values, ap_sims_tscales, 'Timescale',
SIM_ITERS['kn_knee'].values, ap_sims_knee, 'Knee Parameter',
ylabel='Approximate Entropy', color=COLORS['KN'], **fsaver('ap_kn_vars'))
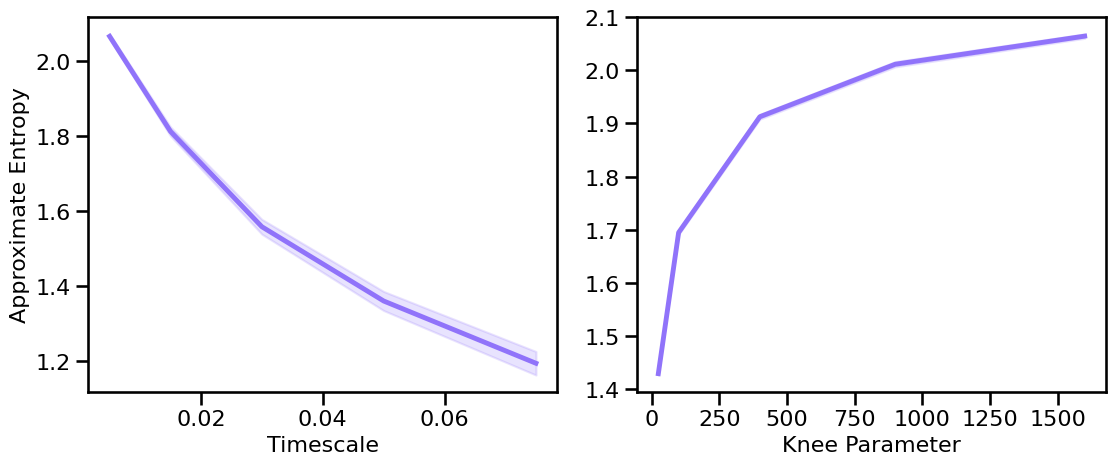
Peak Variations¶
# Run simulations calculating approximate entropy across peak bandwidths (sims from file)
ap_sims_bw = run_sims_load('comb-bw-' + str(fs), app_entropy, AP_ENT_PARAMS)
# Run simulations calculating approximate entropy across burst probabilities
ap_sims_burst = run_sims(sim_combined, SIM_ITERS['comb_burst'], app_entropy, AP_ENT_PARAMS, N_SIMS)
# Plot the estimated approximate entropy across periodic variations
plot_sims_two(SIM_ITERS['peak_bw'].values, ap_sims_bw, 'Bandwidth',
SIM_ITERS['comb_burst'].values, ap_sims_burst, 'Burst Probability',
ylabel='Approximate Entropy', color=COLORS['BW'], **fsaver('ap_pe_vars'))
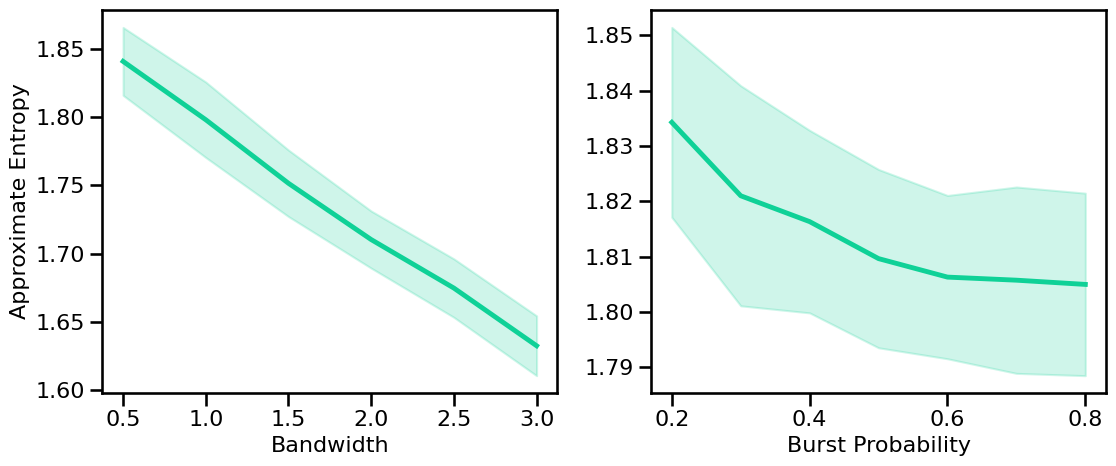
Sample Entropy¶
Sample entropy is a modification of approxmiate entropy for physiological time series.
The modifications of sample entropy make it data length independent.
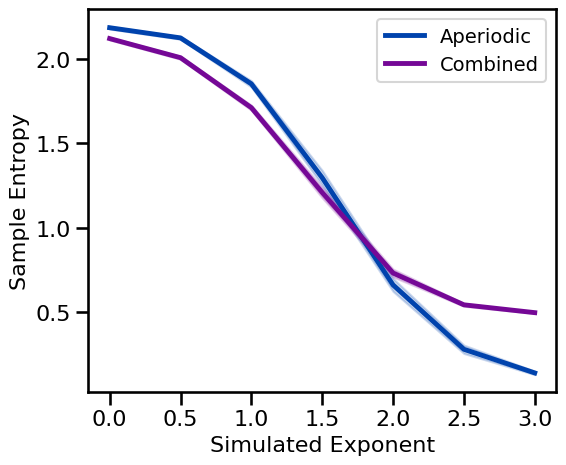
Aperiodic Variations¶
# Run simulations calculating sample entropy across exponents
sa_sims_exp = run_sims(sim_powerlaw, SIM_ITERS['ap_exp'], sample_entropy, SA_ENT_PARAMS, N_SIMS)
# Run simulations calculating sample entropy across exponents, with an oscillation
sa_sims_comb = run_sims(sim_combined, SIM_ITERS['comb_exp'], sample_entropy, SA_ENT_PARAMS, N_SIMS)
# Plot sample entropy measures across aperiodic variations
plot_ap_sims(sa_sims_exp, sa_sims_comb, 'Sample Entropy', **fsaver('sa_ap'))
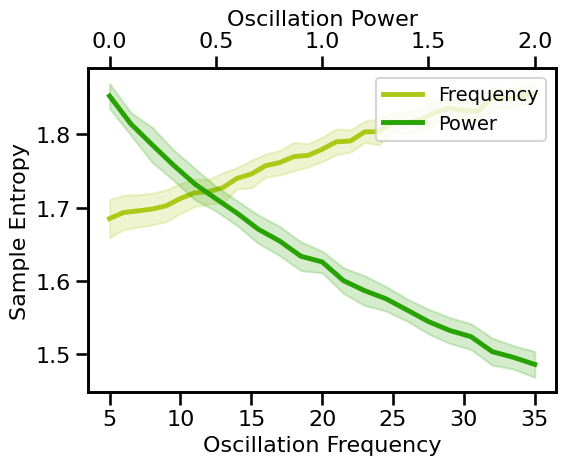
Periodic Variations¶
# Run simulations calculating sample entropy across oscillation frequency
sa_sims_freq = run_sims(\
sim_combined, SIM_ITERS['osc_freq'], sample_entropy, SA_ENT_PARAMS, N_SIMS)
# Run simulations calculating sample entropy across oscillation power
sa_sims_pow = run_sims(\
sim_combined, SIM_ITERS['osc_pow'], sample_entropy, SA_ENT_PARAMS, N_SIMS)
# Plot sample entropy measures across periodic variations
plot_pe_sims(sa_sims_freq, sa_sims_pow, 'Sample Entropy', **fsaver('sa_pe'))
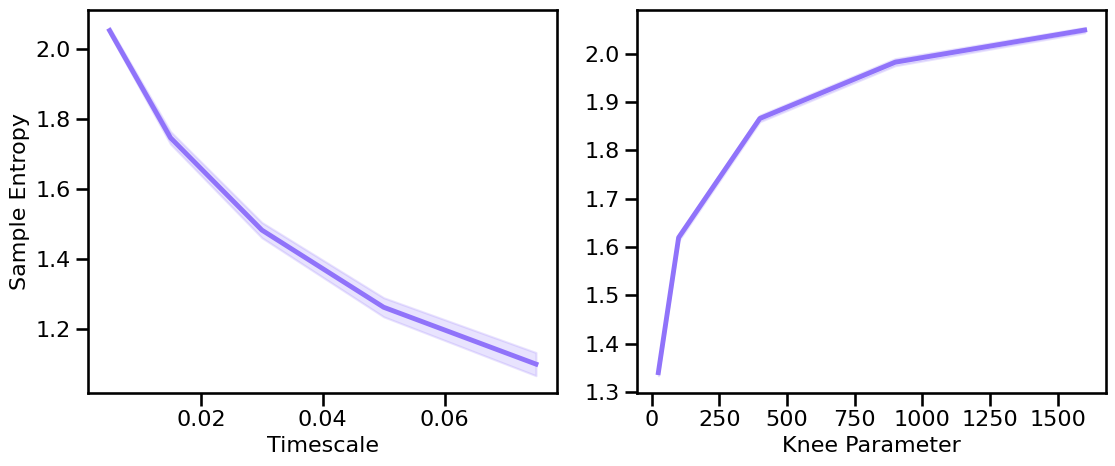
Knee Variations¶
# Run simulations calculating sample entropy across timescales
sa_sims_tscales = run_sims(sim_synaptic_current, SIM_ITERS['syn_tscales'],
sample_entropy, SA_ENT_PARAMS, N_SIMS)
# Run simulations calculating sample exntropy across different knee parameters (sims from file)
sa_sims_knee = run_sims_load('ap-knee-' + str(fs), sample_entropy, SA_ENT_PARAMS)
# Plot the estimated sample entropy across different timescales & knees
plot_sims_two(SIM_ITERS['syn_tscales'].values, sa_sims_tscales, 'Timescale',
SIM_ITERS['kn_knee'].values, sa_sims_knee, 'Knee Parameter',
ylabel='Sample Entropy', color=COLORS['KN'], **fsaver('sa_kn_vars'))
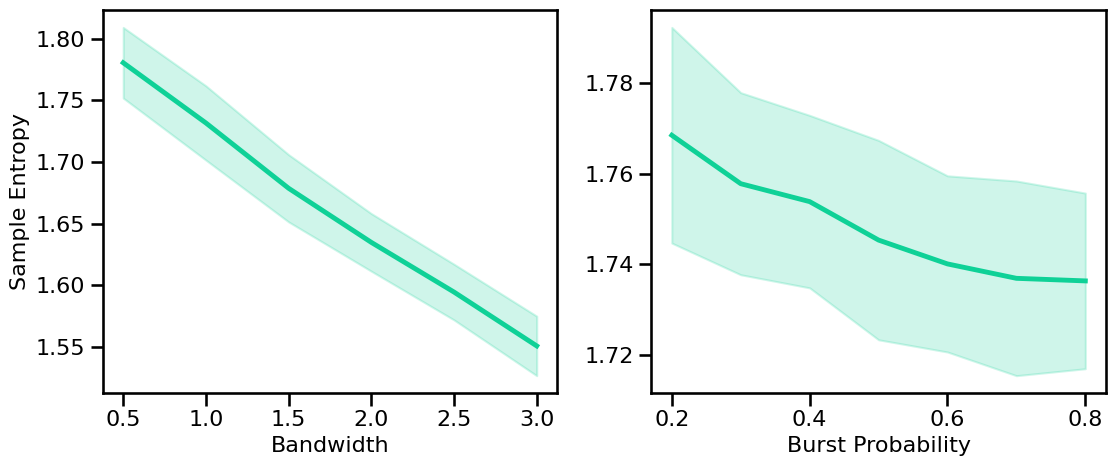
Peak Variations¶
# Run simulations calculating sample entropy across peak bandwidths (sims from file)
sa_sims_bw = run_sims_load('comb-bw-' + str(fs), sample_entropy, SA_ENT_PARAMS)
# Run simulations calculating sample entropy across burst probabilities
sa_sims_burst = run_sims(sim_combined, SIM_ITERS['comb_burst'],
sample_entropy, SA_ENT_PARAMS, N_SIMS)
# Plot the estimated sample entropy across periodic variations
plot_sims_two(SIM_ITERS['peak_bw'].values, sa_sims_bw, 'Bandwidth',
SIM_ITERS['comb_burst'].values, sa_sims_burst, 'Burst Probability',
ylabel='Sample Entropy', color=COLORS['BW'], **fsaver('sa_pe_vars'))
Permutation Entropy¶
Permutation entropy is a measure of entropy based on the probabilities of sequences within the time series.
Permutation entropy was introduced in 2002 by Bandt & Pompe.
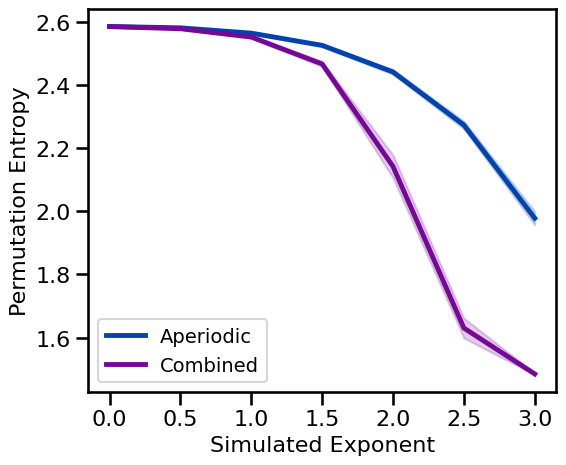
Aperiodic Variations¶
# Run simulations calculating permutation entropy across exponents
pe_sims_exp = run_sims(sim_powerlaw, SIM_ITERS['ap_exp'], perm_entropy, PE_ENT_PARAMS, N_SIMS)
# Run simulations calculating permutation entropy across exponents, with an oscillation
pe_sims_comb = run_sims(sim_combined, SIM_ITERS['comb_exp'], perm_entropy, PE_ENT_PARAMS, N_SIMS)
# Plot permutation entropy measures across periodic variations
plot_ap_sims(pe_sims_exp, pe_sims_comb, 'Permutation Entropy', **fsaver('pe_ap'))
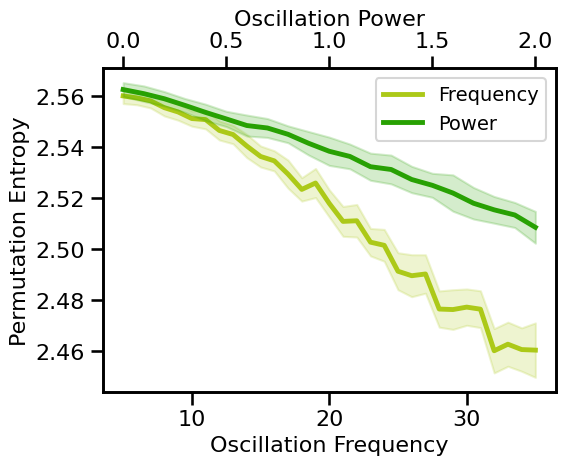
Periodic Variations¶
# Run simulations calculating permutation entropy across oscillation frequency
pe_sims_freq = run_sims(sim_combined, SIM_ITERS['osc_freq'],
perm_entropy, PE_ENT_PARAMS, N_SIMS)
# Run simulations calculating permutation entropy across oscillation power
pe_sims_pow = run_sims(sim_combined, SIM_ITERS['osc_pow'],
perm_entropy, PE_ENT_PARAMS, N_SIMS)
# Plot permutation entropy measures across periodic variations
plot_pe_sims(pe_sims_freq, pe_sims_pow, 'Permutation Entropy', **fsaver('pe_pe'))
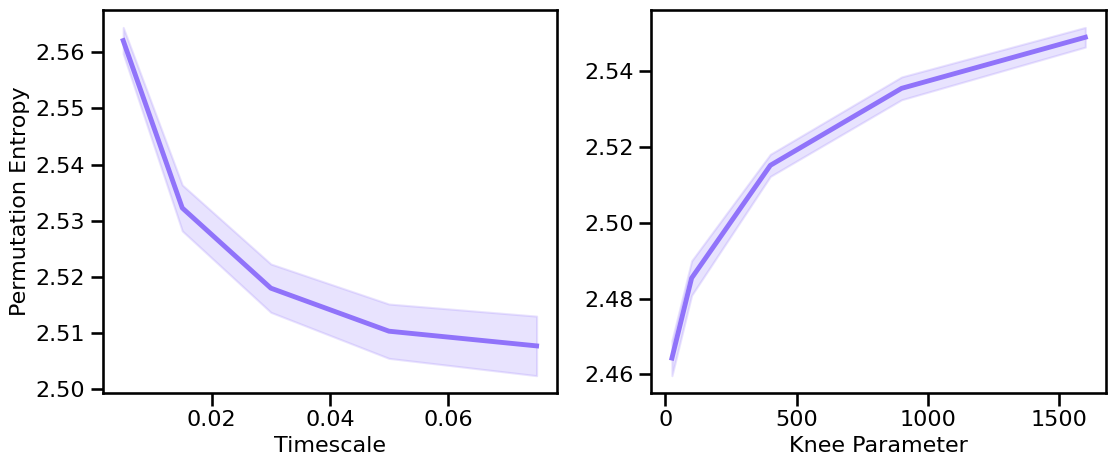
Knee Variations¶
# Run simulations calculating permutation entropy across timescales
pe_sims_tscales = run_sims(sim_synaptic_current, SIM_ITERS['syn_tscales'],
perm_entropy, PE_ENT_PARAMS, N_SIMS)
# Run simulations calculating permutation entropy across different knee parameters (sims from file)
pe_sims_knee = run_sims_load('ap-knee-' + str(fs), perm_entropy, PE_ENT_PARAMS)
# Plot the estimated permutation entropy across different timescales & knees
plot_sims_two(SIM_ITERS['syn_tscales'].values, pe_sims_tscales, 'Timescale',
SIM_ITERS['kn_knee'].values, pe_sims_knee, 'Knee Parameter',
ylabel='Permutation Entropy', color=COLORS['KN'], **fsaver('pe_kn_vars'))
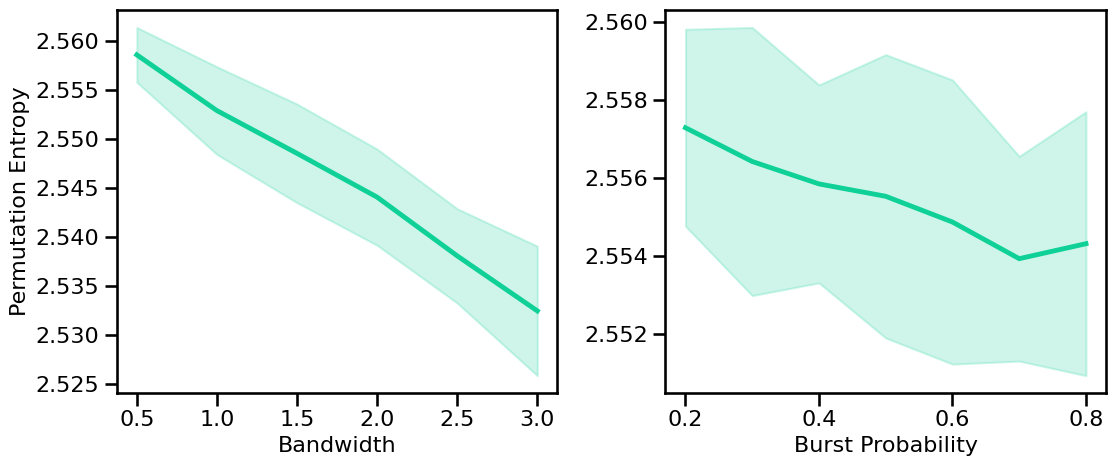
Peak Variations¶
# Run simulations calculating permutation entropy across peak bandwidths (sims from file)
pe_sims_bw = run_sims_load('comb-bw-' + str(fs), perm_entropy, PE_ENT_PARAMS)
# Run simulations calculating permutation entropy across burst probabilities
pe_sims_burst = run_sims(sim_combined, SIM_ITERS['comb_burst'],
perm_entropy, PE_ENT_PARAMS, N_SIMS)
# Plot the estimated permutation entropy across periodic variations
plot_sims_two(SIM_ITERS['peak_bw'].values, pe_sims_bw, 'Bandwidth',
SIM_ITERS['comb_burst'].values, pe_sims_burst, 'Burst Probability',
ylabel='Permutation Entropy', color=COLORS['BW'], **fsaver('pe_pe_vars'))
Weighted Permutation Entropy¶
Aperiodic Variations¶
# Run simulations calculating weighted permutation entropy across exponents
wpe_sims_exp = run_sims(sim_powerlaw, SIM_ITERS['ap_exp'],
wperm_entropy, WPE_ENT_PARAMS, N_SIMS)
# Run simulations calculating weighted permutation entropy across exponents, with an oscillation
wpe_sims_comb = run_sims(sim_combined, SIM_ITERS['comb_exp'],
wperm_entropy, WPE_ENT_PARAMS, N_SIMS)
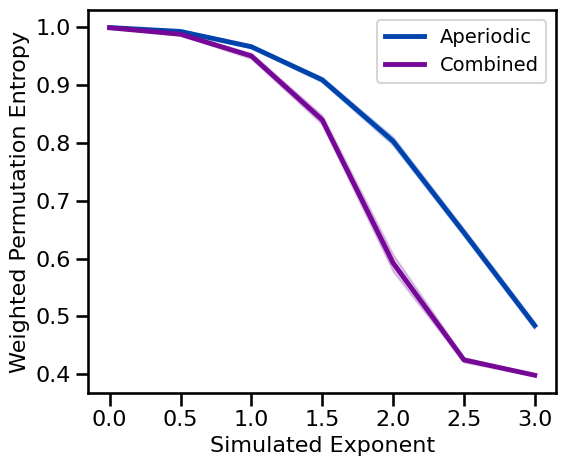
# Plot weighted permutation entropy measures across periodic variations
plot_ap_sims(wpe_sims_exp, wpe_sims_comb, 'Weighted Permutation Entropy', **fsaver('wpe_ap'))
Periodic Variations¶
# Run simulations calculating weighted permutation entropy across oscillation frequency
wpe_sims_freq = run_sims(sim_combined, SIM_ITERS['osc_freq'],
wperm_entropy, WPE_ENT_PARAMS, N_SIMS)
# Run simulations calculating weighted permutation entropy across oscillation power
wpe_sims_pow = run_sims(sim_combined, SIM_ITERS['osc_pow'],
wperm_entropy, WPE_ENT_PARAMS, N_SIMS)
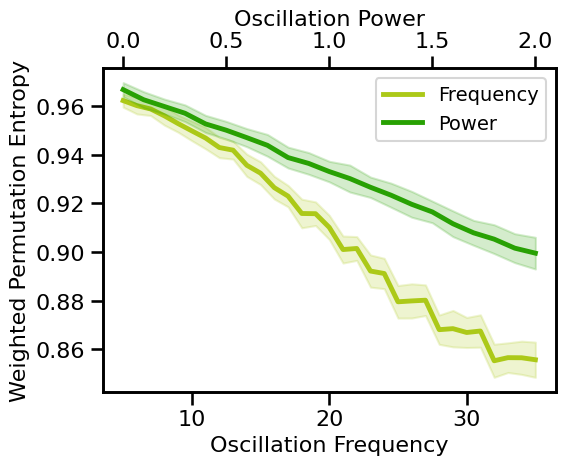
# Plot weighted permutation entropy measures across periodic variations
plot_pe_sims(wpe_sims_freq, wpe_sims_pow, 'Weighted Permutation Entropy', **fsaver('wpe_pe'))
Knee Variations¶
# Run simulations calculating weighted permutation entropy across timescales
wpe_sims_tscales = run_sims(sim_synaptic_current, SIM_ITERS['syn_tscales'],
wperm_entropy, WPE_ENT_PARAMS, N_SIMS)
# Run simulations calculating weighted permutation exntropy across knee parameters (sims from file)
wpe_sims_knee = run_sims_load('ap-knee-' + str(fs), wperm_entropy, WPE_ENT_PARAMS)
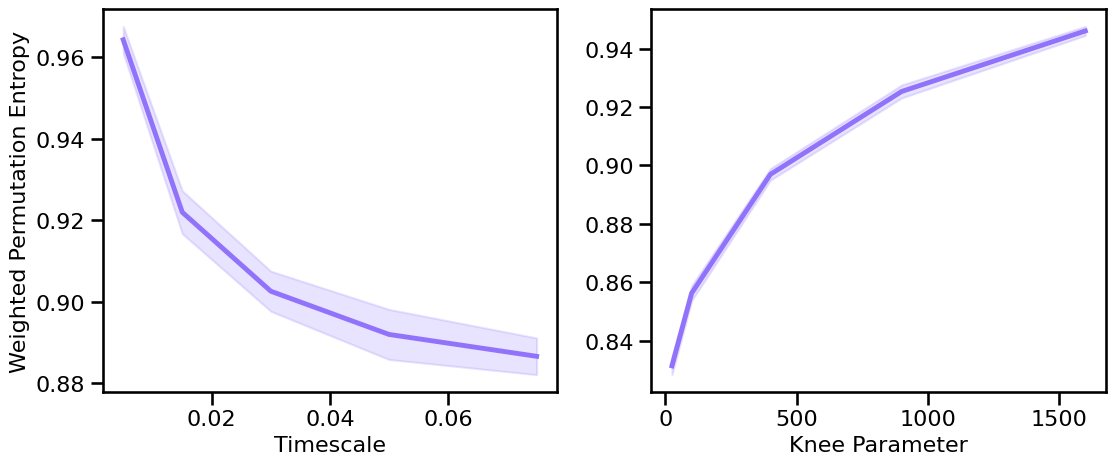
# Plot the estimated weighted permutation entropy across different timescales & knees
plot_sims_two(SIM_ITERS['syn_tscales'].values, wpe_sims_tscales, 'Timescale',
SIM_ITERS['kn_knee'].values, wpe_sims_knee, 'Knee Parameter',
ylabel='Weighted Permutation Entropy', color=COLORS['KN'], **fsaver('wpe_kn_vars'))
Peak Variations¶
# Run simulations calculating weighted permutation entropy across peak bandwidths (sims from file)
wpe_sims_bw = run_sims_load('comb-bw-' + str(fs), wperm_entropy, WPE_ENT_PARAMS)
# Run simulations calculating weighted permutation entropy across burst probabilities
wpe_sims_burst = run_sims(sim_combined, SIM_ITERS['comb_burst'],
wperm_entropy, WPE_ENT_PARAMS, N_SIMS)
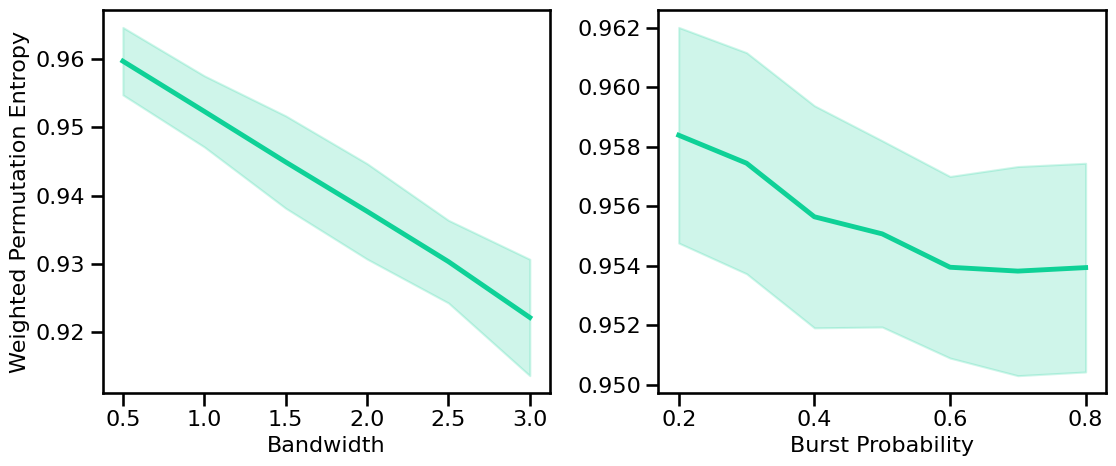
# Plot the estimated weighted permutation entropy across periodic variations
plot_sims_two(SIM_ITERS['peak_bw'].values, wpe_sims_bw, 'Bandwidth',
SIM_ITERS['comb_burst'].values, wpe_sims_burst, 'Burst Probability',
ylabel='Weighted Permutation Entropy', color=COLORS['BW'], **fsaver('wpe_pe_vars'))
Conclusions¶
Overall, we can see the following patterns in these simulations:
Entropy (general patterns across all):
Entropy increases for decreasing aperiodic exponents, non-linearly
Entropy decreases for increasing oscillatory power, approximately linearly