Spectral Fitting
Contents
Spectral Fitting¶
This notebook measures aperiodic activity using various different spectral fitting measures.
There have been many variations for fitting power spectra. This notebook compares different strategies.
This notebooks covers:
Linear fits to power spectra in log-log spacing, using a simple (OLS) linear fit
Linear fits to power spectra in log-log spacing, using a robust (RLM) linear fit
Linear fits to power spectra in log-log spacing, using the RANSAC robust fitting algorithm
Exponential fits to power spectra in semi-log spacing, using a simple exponential fit
The spectral parameterization method
In addition, various studies have used simple heuristics to try and fit aperiodic activity while avoiding being biased by peaks.
In this comparison, we include the following variations of the aforementioned methods:
Fitting the entire frequency range
Using a predefined exclusion zone of the alpha oscillation (7-14 Hz)
Using exclusing zones for all oscillatory peaks*
*Note that in the oscillation exclusion approach, the spectral parameterization method is initially used to detect and exclude oscillatory regions. Therefore, these are not fully independent methods, but are instead used to evaluate if there could be any improved fitting after oscillation exclusion.
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.optimize import curve_fit
from sklearn.linear_model import RANSACRegressor
from scipy.stats.mstats import normaltest
from fooof import FOOOF
from fooof.core.funcs import expo_nk_function as expf
from fooof.sim import gen_power_spectrum, gen_group_power_spectra
# Import custom code
import sys; from pathlib import Path
sys.path.append(str(Path('..').resolve()))
from apm.methods import SpectralFits
from apm.methods.fit import *
from apm.plts import plot_psds, plot_psds_two, plot_psds_shades
from apm.plts.errors import plot_violin_errors, plot_boxplot_errors, plot_corr_matrix
from apm.plts.utils import color_red_or_green
from apm.utils import exclude_spectrum, print_results
from apm.core.db import APMDB
from apm.core.io import save_pickle, load_pickle
from apm.sim.peaks import *
Settings¶
# Set up project database object
db = APMDB()
# Simulation settings
f_range = [1, 50]
off_val = 0
noise = 0.0
# Notebook Settings
SAVE_FIG = False
SAVE_DATA = False
RERUN = False # If False, reloads previously computed measures
Spectral Fitting Methods¶
Here we demonstrate spectral fitting methods for measuring the aperiodic exponent by directly fitting power spectra.
The implementations of these methods are available in apm/fit.py.
Example PSD¶
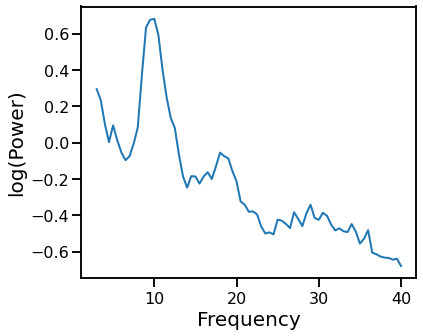
Load an example PSD, from eyes closed, resting state EEG data, extracted to the range of 3-40 Hz.
# Load an example power spectrum to check fitting with
freqs = np.load('data/freqs.npy')
psd = np.load('data/psd.npy')
# Check a plot of the loaded power spectrum
plot_psds(freqs, psd)
Methods for Fitting Power Spectra¶
Here, we introduce the various methods for fitting the aperiodic component of the power spectrum.
# Initialize for collecting example fit results
example_results = {}
# Add constant for fitting with statsmodels
fx = sm.add_constant(np.log10(freqs))
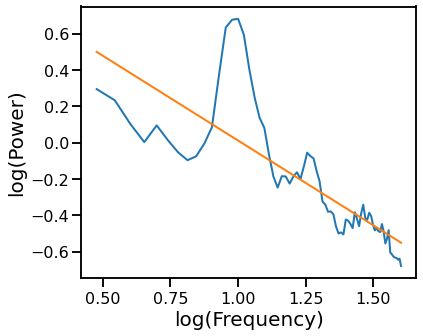
OLS Linear Fit¶
Fit a line in log-log with Ordinary Least Squares (OLS).
# Spectral fit: linear fit
ex_fit_ols = sm.OLS(np.log10(psd), fx).fit()
example_results['ols'] = ex_fit_ols.params[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_fit_ols.fittedvalues)
# Plot the aperiodic fit, from the OLS linear fit
plot_psds(freqs, [psd, pred_vals], log_freqs=True)
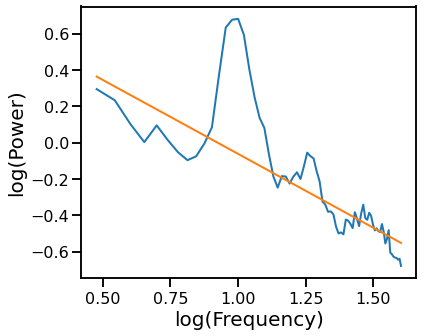
Robust Fit with RLM¶
# Spectral fit: robust linear fit to log-log PSD
ex_fit_rlm = sm.RLM(np.log10(psd), fx).fit()
example_results['rlm'] = ex_fit_rlm.params[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_fit_rlm.fittedvalues)
# Plot the aperiodic fit, from the robust linear fit
plot_psds(freqs, [psd, pred_vals], log_freqs=True)
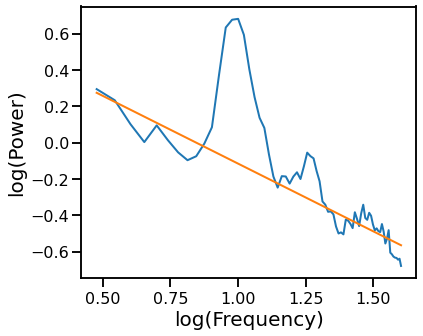
Robust Fit with RANSAC¶
# Reshape freqs for RANSAC fit
freqs_ran = freqs.reshape([len(freqs), 1])
# Initialize and fit with RANSAC
ex_ransac_model = RANSACRegressor()
ex_ransac_model.fit(np.log10(freqs_ran), np.log10(psd))
example_results['ran'] = ex_ransac_model.estimator_.coef_[0]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_ransac_model.predict(np.log10(freqs_ran)))
# Plot the aperiodic fit, from RANSAC
plot_psds(freqs_ran.flatten(), [psd, pred_vals], log_freqs=True)
Spectral Fitting Excluding Alpha¶
Use a specific exclusion zone for the alpha oscillation.
# Exclude predefined alpha range
freqs_alph, psd_alph = exclude_spectrum(np.squeeze(freqs), psd, [7, 14])#, False)
# Reset freqs, with constant
fx_alph = sm.add_constant(np.log10(freqs_alph))
Simple OLS Linear Fit Exlucing Generic Alpha Band¶
# Linear fit without alpha range
ex_fit_ols_alph = sm.OLS(np.log10(psd_alph), fx_alph).fit()
example_results['ols_alph'] = ex_fit_ols_alph.params[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_fit_ols_alph.fittedvalues)
# Plot the aperiodic fit, from an OLS linear fit with an alpha exclusion zone
plot_psds([freqs, freqs_alph], [psd, pred_vals], log_freqs=True)
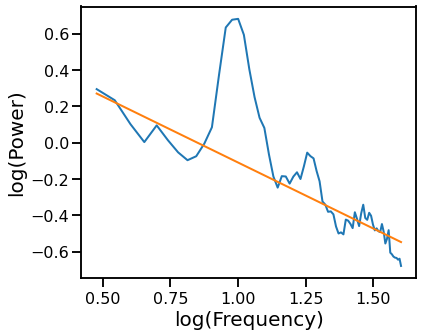
Robust Fit with RLM Excluding Generic Alpha Band¶
# Robust fit without alpha range
ex_fit_rlm_alph = sm.RLM(np.log10(psd_alph), fx_alph).fit()
example_results['rlm_alph'] = ex_fit_rlm_alph.params[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_fit_rlm_alph.fittedvalues)
# Plot the aperiodic fit, from the robust linear fit with an alpha exclusion zone
plot_psds([freqs, freqs_alph], [psd, pred_vals], log_freqs=True)
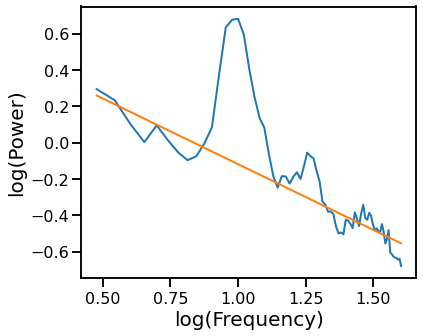
Robust Fit with RANSAC Excluding Generic Alpha Band¶
# Fit alpha-exclusion with RANSAC
ex_ransac_model_alph = RANSACRegressor()
ex_ransac_model_alph.fit(np.log10(freqs_alph), np.log10(psd_alph))
example_results['ran_alph'] = ex_ransac_model_alph.estimator_.coef_[0][0]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_ransac_model_alph.predict(np.log10(freqs_alph)))
# Plot the aperiodic fit, from the RANSAC fit with alpha exclusion zone
plot_psds([freqs, freqs_alph], [psd, pred_vals], log_freqs=True)
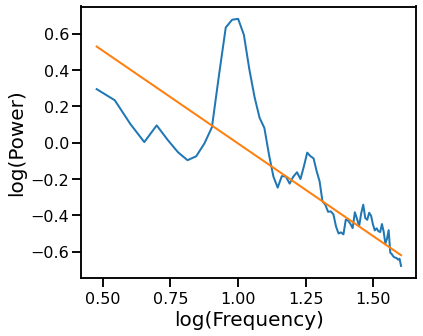
Spectral Fit Excluding Oscillations¶
Use a exclusion zones for oscillations.
# Fit spectral model for finding peaks
fm = FOOOF(peak_width_limits=[1, 8])
fm.fit(freqs, psd, [3, 40])
# Get oscillation definitions from FOOOF
cens = fm.gaussian_params_[:, 0]
bws = fm.gaussian_params_[:, 2]
# Define oscillation ranges, as a range around each center frequency
m = 2
osc_ranges = [[cen-m*bw, cen+m*bw] for cen, bw in zip(cens, bws)]
# Plot PSD with oscillatory regions shaded
plot_psds_shades(freqs, psd, osc_ranges)
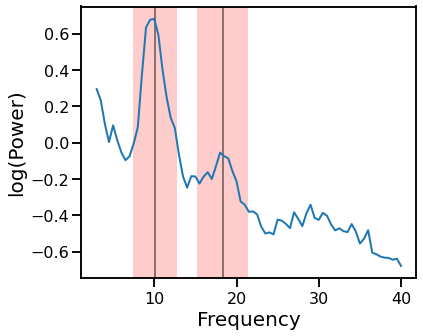
# Exclude oscillation bands, as measured from FOOOF
psd_excl = psd
freqs_excl = np.squeeze(freqs)
for cen, bw in zip(cens, bws):
freqs_excl, psd_excl = exclude_spectrum(freqs_excl, psd_excl, [cen-m*bw, cen+m*bw])
# Create a frequency vector with exlcusion zones for model fitting
fx_excl = sm.add_constant(np.log10(freqs_excl))
Simple Linear Fit Excluding Oscillatory Bands¶
# Linear fit without alpha range
ex_fit_ols_excl = sm.OLS(np.log10(psd_excl), fx_excl).fit()
example_results['ols_excl'] = ex_fit_ols_excl.params[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_fit_ols_excl.fittedvalues)
# Plot the aperiodic fit, from the OLS linear fit with oscillation exclusion zones
plot_psds([freqs, freqs_excl], [psd, pred_vals], log_freqs=True)
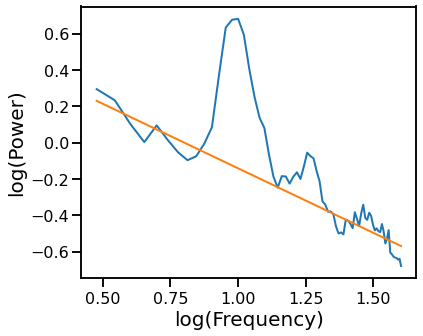
Robust Fit with RLM Excluding Oscillatory Bands¶
# Robust fit without oscillation bands
ex_fit_rlm_excl = sm.RLM(np.log10(psd_excl), fx_excl).fit()
example_results['rlm_excl'] = ex_fit_rlm_excl.params[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_fit_rlm_excl.fittedvalues)
# Plot the aperiodic fit, from the robust linear fit with oscillation exclusion zones
plot_psds([freqs, freqs_excl], [psd, pred_vals], log_freqs=True)
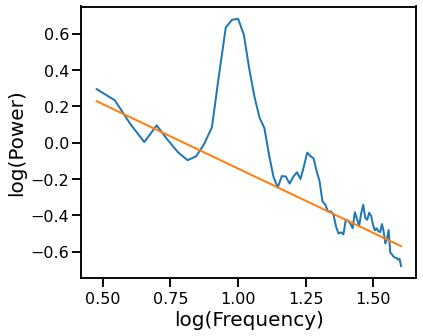
Robust Fit with RANSAC Excluding Oscillatory Bands¶
# Fit alpha-exclusion with RANSAC
ex_ransac_model_excl = RANSACRegressor()
ex_ransac_model_excl.fit(np.log10(freqs_excl), np.log10(psd_excl))
example_results['ran_excl'] = ex_ransac_model_excl.estimator_.coef_[0][0]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, ex_ransac_model_excl.predict(np.log10(freqs_excl)))
# Plot the aperiodic fit, from the RANSAC fit with oscillation exclusion zones
plot_psds([freqs, freqs_excl], [psd, pred_vals], log_freqs=True)
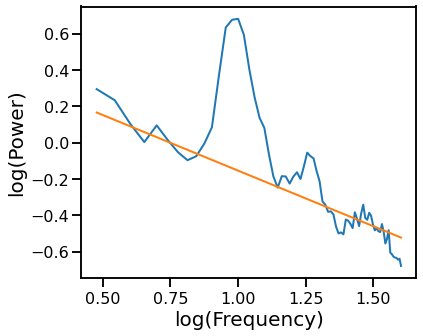
Exponential Fits¶
Exponential Fit¶
# Fit exponential 1/f, with scipy curve_fit
ex_fit_exp, _ = curve_fit(expf, np.squeeze(freqs), np.squeeze(np.log10(psd)), p0=[1, 1])
example_results['exp'] = -ex_fit_exp[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, expf(freqs, *ex_fit_exp))
# Plot the aperiodic fit, from the exponential fit
plot_psds(freqs.flatten(), [psd, pred_vals], log_freqs=True)
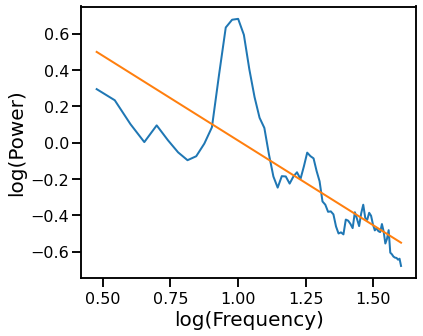
Exponential Fit Excluding Alpha Region¶
# Fit exponential 1/f, with scipy curve_fit, excluding alpha range
ex_fit_exp_alph, _ = curve_fit(expf, np.squeeze(freqs_alph), np.squeeze(np.log10(psd_alph)), p0=[1, 1])
example_results['exp_alph'] = -ex_fit_exp_alph[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, expf(freqs_alph, *ex_fit_exp_alph))
# Plot the aperiodic fit, from the exponential fit, with an alpha exclusion zone
plot_psds([freqs, freqs_alph], [psd, pred_vals], log_freqs=True)
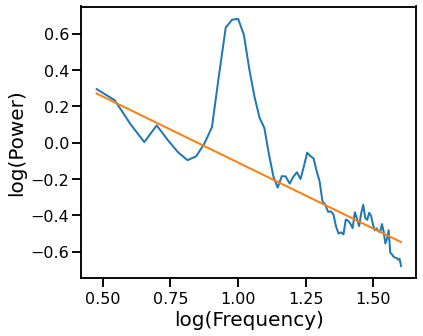
Exponential Fit Excluding Oscillation Regions¶
# Fit exponential 1/f, with scipy curve_fit, excluding oscillatory regions
ex_fit_exp_excl, _ = curve_fit(expf, np.squeeze(freqs_excl), np.squeeze(np.log10(psd_excl)), p0=[1, 1])
example_results['exp_excl'] = -ex_fit_exp_excl[1]
# Get the predicted values of the aperiodic fit
pred_vals = np.power(10, expf(freqs_excl, *ex_fit_exp_excl))
# Plot the aperiodic fit, from the exponential fit with oscillation exclusion zones
plot_psds([freqs, freqs_excl], [psd, pred_vals], log_freqs=True)
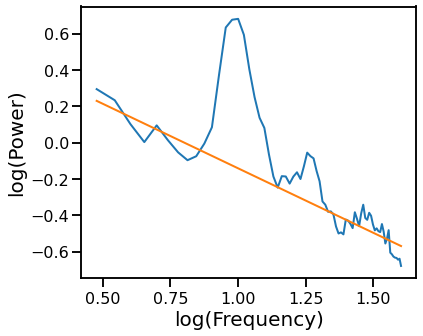
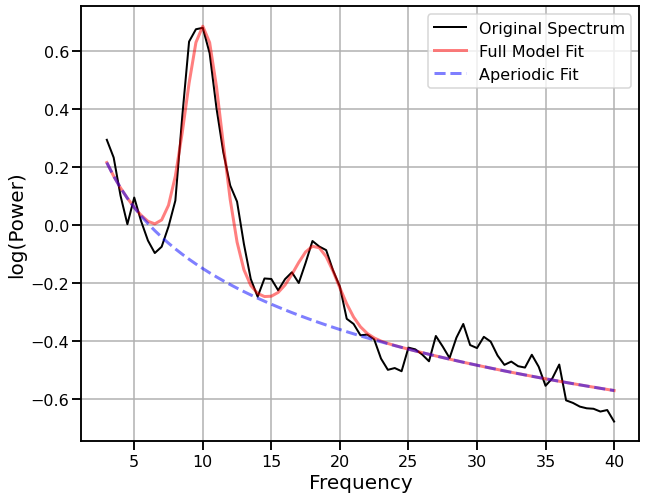
Spectral Parameterization¶
# Fit the SpecParam model
fm = FOOOF(verbose=False)
fm.report(freqs, psd, [3, 40])
example_results['fooof'] = -fm.aperiodic_params_[1]
==================================================================================================
FOOOF - POWER SPECTRUM MODEL
The model was run on the frequency range 3 - 40 Hz
Frequency Resolution is 0.50 Hz
Aperiodic Parameters (offset, exponent):
0.5498, 0.6997
2 peaks were found:
CF: 10.07, PW: 0.837, BW: 2.67
CF: 18.31, PW: 0.259, BW: 3.10
Goodness of fit metrics:
R^2 of model fit is 0.9655
Error of the fit is 0.0510
==================================================================================================
Compare Example Fits¶
# Print out results across all the different approaches
print('FIT RESULTS')
for key, val in example_results.items():
print(' {:10s} \t {:1.3f}'.format(key, val))
FIT RESULTS
ols -0.933
rlm -0.813
ran -0.746
ols_alph -0.726
rlm_alph -0.723
ran_alph -1.020
ols_excl -0.710
rlm_excl -0.709
ran_excl -0.612
exp -0.933
exp_alph -0.726
exp_excl -0.710
fooof -0.700
# Check fits ordered by magnitude
for key, val in dict(sorted(example_results.items(), key=lambda it: it[1])).items():
print('{:10s} \t {:1.5f}'.format(key, val))
ran_alph -1.02043
ols -0.93306
exp -0.93306
rlm -0.81338
ran -0.74555
exp_alph -0.72646
ols_alph -0.72646
rlm_alph -0.72290
exp_excl -0.70999
ols_excl -0.70999
rlm_excl -0.70878
fooof -0.69973
ran_excl -0.61167
Simulation Tests¶
Now that we have introduced the different methods, we will systematically evaluatate them across simulated data.
# Initialize and set up for simulated data testing
fits = SpectralFits()
# Check the fitting functions being used
print(fits.labels)
['OLS', 'OLS-EA', 'OLS-EO', 'RLM', 'RLM-EA', 'RLM-EO', 'RAN', 'RAN-EA', 'RAN-EO', 'EXP', 'EXP-EA', 'EXP-EO', 'SPECPARAM']
Check out PSD generation and test fitting¶
# Generate a single simulated test power spectrum
exp_val = 1
peak_gen = gen_peak_def()
peaks = next(peak_gen)
# Simulate an example power spectrum
freqs, psd = gen_power_spectrum(f_range, [off_val, exp_val], peaks, noise)
# Plot and check a simulated spectrum, plotted in semi-log and log space
plot_psds_two(freqs, psd, np.log10(freqs), np.log10(psd))
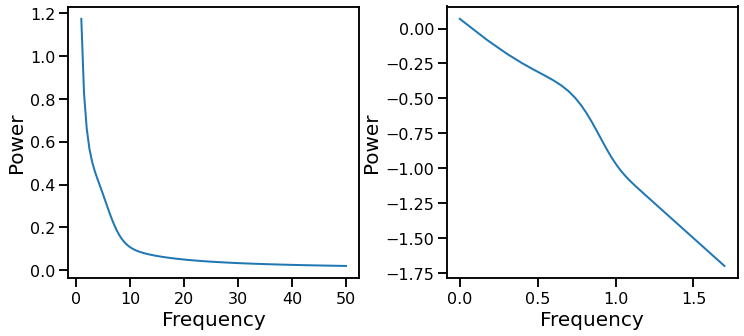
# Check example fits
print('Example fits for true exponent value of {:d}:'.format(exp_val))
for name, func in fits.fit_funcs.items():
print(' {:5s} \t {:1.3f}'.format(name, func(freqs, psd)))
Example fits for true exponent value of 1:
OLS -1.138
OLS-EA -1.141
OLS-EO -1.039
RLM -1.089
RLM-EA -1.086
RLM-EO -1.002
RAN -1.089
RAN-EA -1.077
RAN-EO -1.039
EXP -1.138
EXP-EA -1.141
EXP-EO -1.039
SPECPARAM -1.054
Run Spectral Fits on Simulated Power Spectra¶
Run spectral fitting across multiple exponents and noise levels.
# Spectrum Settings
N_SPECTRA = 50
F_RANGE = [1, 50]
# Simulation Settings
NOISE_VALS = [0.0, 0.01, 0.05, 0.1, 0.15, 0.2, 0.25]
EXP_VALS = [0.5, 1.0, 1.5, 2.0, 2.5, 3.0]
# Set verbose setting
VERBOSE = False
# Run all fits
if RERUN:
all_fits = SpectralFits()
for exp in EXP_VALS:
for noise in NOISE_VALS:
if VERBOSE:
print('Running sims for exponent val {}, noise-val {}'.format(exp, noise))
# Simulate set of power spectra
freqs, psds, sim_params = gen_group_power_spectra(\
N_SPECTRA, F_RANGE, [off_val, exp], gen_peak_def(), noise, return_params=True)
# Initialize SimFit object, and run fits
fits = SpectralFits()
fits.fit_spectra(exp, freqs, psds)
# Collect results together
all_fits = all_fits + fits
# Save out fit data
if SAVE_DATA:
save_name = 'SpectralFits_exp' + str(exp) + '_N' + str(noise) + '.p'
save_pickle(fits.errors, save_name, db.sims_path)
else:
# Get list of simulated fit results files
sim_files = db.check_files('sims')
# Reload and combine all fit files
all_fits = SpectralFits()
for f_name in sim_files:
temp = SpectralFits()
temp.errors = load_pickle(f_name, db.sims_path)
all_fits = all_fits + temp
# Check list of available fit files
#sim_files = db.check_files('sims')
#sim_files
# # Load specific spectral fits
# f_ind = 0
# fits = SpectralFits()
# fits.errors = load_pickle(sim_files[f_ind], db.sims_path)
Compare Spectral Fitting¶
# Check how many PSDs are included in simulated data model fits
print(len(all_fits))
2100
# Check the average errors per method
print('Average error for each method:')
avg_errors = all_fits.compute_avg_errors(avg='mean')
print_results(avg_errors)
Average error for each method:
RLM-EO 0.04816
EXP-EO 0.05024
OLS-EO 0.05024
SPECPARAM 0.05396
RLM-EA 0.06848
RAN-EO 0.08225
EXP-EA 0.08927
OLS-EA 0.08927
RAN-EA 0.09850
RLM 0.10139
RAN 0.11743
OLS 0.13121
EXP 0.13121
# Check the standard deviation of errors per method
print('Standard deviation of the errors for each method:')
std_errors = all_fits.compute_std_errors()
print_results(std_errors)
Standard deviation of the errors for each method:
SPECPARAM 0.07266
EXP-EO 0.07879
OLS-EO 0.07879
RLM-EO 0.07940
RLM-EA 0.12418
OLS-EA 0.13829
EXP-EA 0.13829
RAN-EO 0.15229
RLM 0.16105
OLS 0.17543
EXP 0.17543
RAN 0.21396
RAN-EA 0.26758
# Check the number of fits that pass a threshold, per method
print('Percentage of fits below an error threshold:')
print_results(all_fits.compute_threshold(thresh=0.05))
Percentage of fits below an error threshold:
RLM-EO 69.28571
OLS-EO 68.09524
EXP-EO 68.09524
RLM-EA 64.52381
SPECPARAM 64.42857
RAN-EO 60.00000
RAN-EA 59.04762
OLS-EA 54.19048
EXP-EA 54.19048
RLM 53.85714
RAN 49.14286
OLS 43.57143
EXP 43.57143
# Check the number of fits that pass a threshold, per method
print('Percentage of fits above an error threshold:')
print_results(all_fits.compute_threshold(thresh=0.5, direction='above'))
Percentage of fits above an error threshold:
OLS 5.00000
EXP 5.00000
RAN 4.19048
RLM 3.66667
RAN-EA 3.09524
OLS-EA 2.90476
EXP-EA 2.90476
RLM-EA 2.09524
RAN-EO 1.90476
RLM-EO 0.28571
OLS-EO 0.23810
EXP-EO 0.23810
SPECPARAM 0.19048
Visualizations¶
# Define labels
mains = ['OLS', 'RLM', 'RAN', 'EXP', 'SPECPARAM']
alphas = ['OLS-EA', 'RLM-EA', 'RAN-EA', 'EXP-EA', 'SPECPARAM']
oscs = ['OLS-EO', 'RLM-EO', 'RAN-EO', 'EXP-EO', 'SPECPARAM']
# Split up methods by approach
main_dicts = {label : all_fits.errors[label] for label in mains}
alphas_dicts = {label : all_fits.errors[label] for label in alphas}
oscs_dicts = {label : all_fits.errors[label] for label in oscs}
Violin Plots¶
# Plot settings
ylim = [0, 0.75]
plot_violin_errors(main_dicts, ylim=ylim)
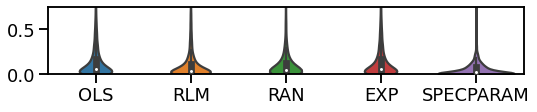
plot_violin_errors(alphas_dicts, ylim=ylim)
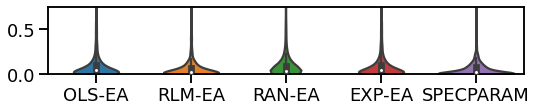
plot_violin_errors(oscs_dicts, ylim=ylim)

# Violin plot of error distributions
plot_violin_errors(all_fits.errors, ylim=[0, 1.5], figsize=[15, 4])
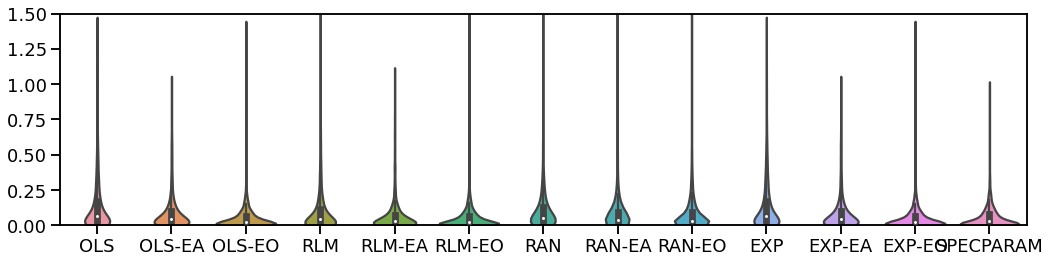
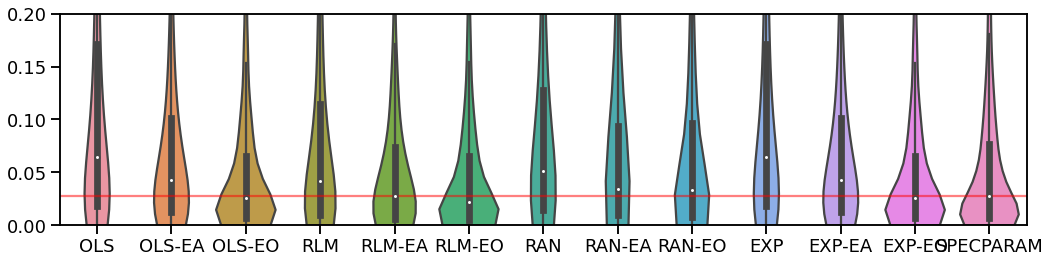
# Plot violin plots zoomed in
plot_violin_errors(all_fits.errors, ylim=[0, 0.2], figsize=[15, 4])
plt.gca().axhline(np.nanmedian(all_fits.errors['SPECPARAM']), color='red', alpha=0.5)
<matplotlib.lines.Line2D at 0x7fa1288ec640>
Statistically Compare Methods¶
# Create a dataframe of the simulation errors
errors_df = pd.DataFrame(all_fits.errors)
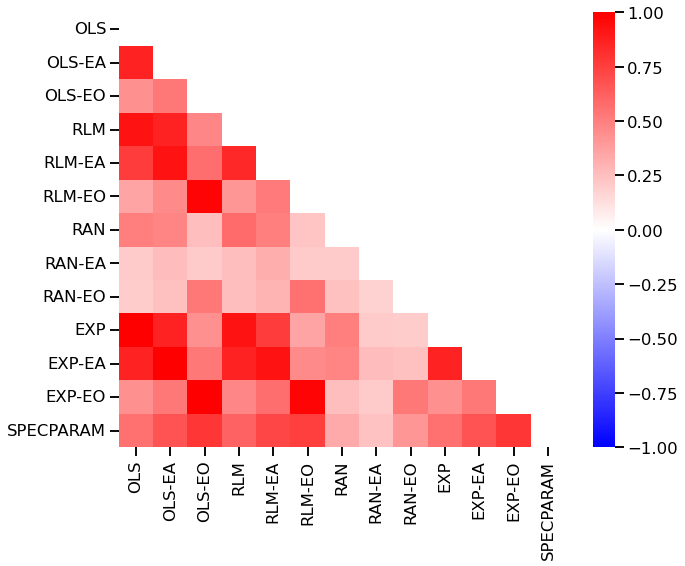
# Check the correlation structure between fit errors
plot_corr_matrix(errors_df.corr())
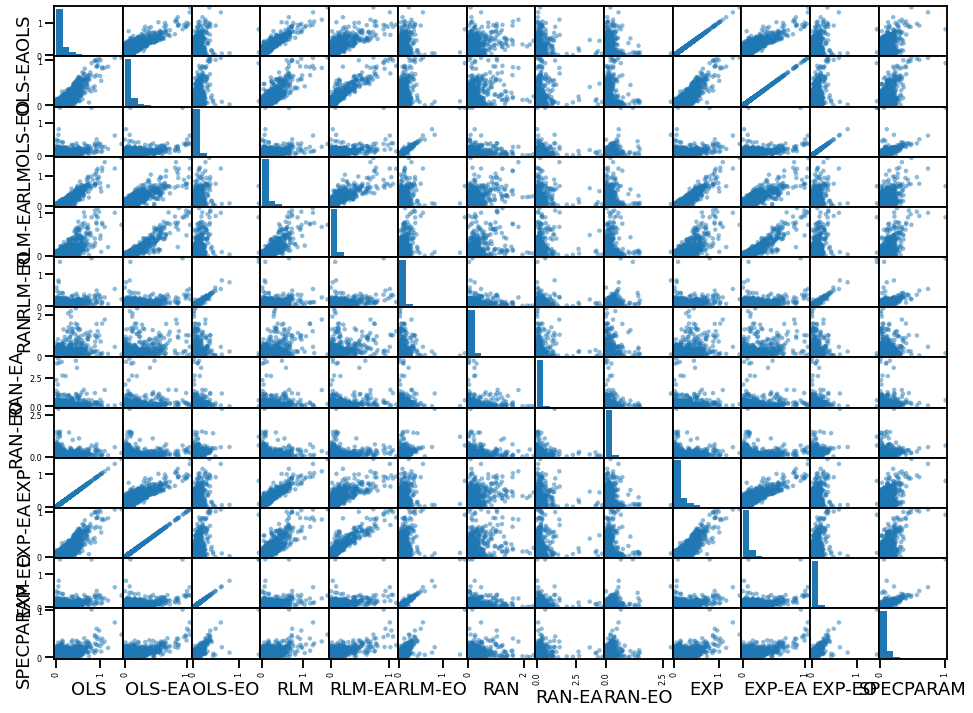
# Plot data distributions and inter-relations
pd.plotting.scatter_matrix(errors_df, figsize=[16, 12]);
# # Apply a normal test across fit-error distributions
# normalities = errors_df.apply(normaltest)
# # Check which results of normal test
# nt_df = pd.DataFrame([data[1] for data in normalities.values], index=normalities.index)
# nt_df.style.applymap(color_red_or_green)
# Run comparisons between methods
comps = all_fits.compare_errors()
# Print out color-coded dataframe of comparison results
comps_df = pd.DataFrame(comps, index=all_fits.errors.keys(), columns=all_fits.errors.keys())
comps_df.style.applymap(color_red_or_green)
| OLS | OLS-EA | OLS-EO | RLM | RLM-EA | RLM-EO | RAN | RAN-EA | RAN-EO | EXP | EXP-EA | EXP-EO | SPECPARAM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OLS | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000003 | 0.000000 | 0.000000 | 0.939383 | 0.000000 | 0.000000 | 0.000000 |
| OLS-EA | 0.000000 | 1.000000 | 0.000000 | 0.941894 | 0.000000 | 0.000000 | 0.000315 | 0.000591 | 0.000048 | 0.000000 | 0.939828 | 0.000000 | 0.000000 |
| OLS-EO | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.205338 | 0.004267 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.938208 | 0.070900 |
| RLM | 0.000000 | 0.941894 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000673 | 0.002725 | 0.000293 | 0.000000 | 0.853769 | 0.000000 | 0.000000 |
| RLM-EA | 0.000000 | 0.000000 | 0.205338 | 0.000000 | 1.000000 | 0.000088 | 0.000000 | 0.000002 | 0.000050 | 0.000000 | 0.000000 | 0.250478 | 0.593834 |
| RLM-EO | 0.000000 | 0.000000 | 0.004267 | 0.000000 | 0.000088 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.002891 | 0.000004 |
| RAN | 0.000003 | 0.000315 | 0.000000 | 0.000673 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000003 | 0.000336 | 0.000000 | 0.000000 |
| RAN-EA | 0.000000 | 0.000591 | 0.000000 | 0.002725 | 0.000002 | 0.000000 | 0.000000 | 1.000000 | 0.460585 | 0.000000 | 0.000538 | 0.000000 | 0.000007 |
| RAN-EO | 0.000000 | 0.000048 | 0.000000 | 0.000293 | 0.000050 | 0.000000 | 0.000000 | 0.460585 | 1.000000 | 0.000000 | 0.000044 | 0.000000 | 0.000135 |
| EXP | 0.939383 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000003 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 |
| EXP-EA | 0.000000 | 0.939828 | 0.000000 | 0.853769 | 0.000000 | 0.000000 | 0.000336 | 0.000538 | 0.000044 | 0.000000 | 1.000000 | 0.000000 | 0.000000 |
| EXP-EO | 0.000000 | 0.000000 | 0.938208 | 0.000000 | 0.250478 | 0.002891 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.082048 |
| SPECPARAM | 0.000000 | 0.000000 | 0.070900 | 0.000000 | 0.593834 | 0.000004 | 0.000000 | 0.000007 | 0.000135 | 0.000000 | 0.000000 | 0.082048 | 0.999401 |
Conclusions¶
Overall, we can see the following patterns in these simulations:
Line fitting:
In general, the methods perform quite similarly in terms of average error, but have different variances of the errors
Standard robust fitting measures are not necessarily better for measuring aperiodic exponent
Overall, the spectral parameterization approach offers low average error and few outliers